前言#
我们常说聚类(Clustering)是迈入无监督学习大门的钥匙,但大多数教材只讲 K-Means,轻轻一笔带过 K-Medoids。
但其实:
-
K-Means 虽然快,但很容易被离群点/极端值干扰;
-
而 K-Medoids 则是更稳健、更抗噪声的一种聚类方式,特别适合我们面对“有点乱”的现实数据时使用,而且在真实场景和社会科学领域中,反倒会比K-Means用途更广。
如果你已经学过 K-Means,本篇会让你:
-
更好地理解“代表点”的意义;
-
看懂 K-Medoids 每一步怎么优化的;
-
彻底搞清楚为什么它更“稳”,但也更“慢”。
目录(可点击跳转)#
概念解释#
什么是 K-medoids?#
K-Medoids 是一种聚类算法,和 K-Means 很像,但是更“稳”。
想象你有一堆朋友(数据点),你想把他们分成几个小团体(簇),每个团体有个“带头大哥”(英文叫做medoid)。这个“带头大哥”不是随便选的,他必须是朋友中的一个,而且要让团体里每个人到他的“距离”总和尽量小。K-medoids 的目标就是找到这些“带头大哥”,让所有团体都尽量紧凑。
和 K-means 的区别?#
K-means 的“中心”是算出来的平均值,可能不是真实的数据点;而 k-medoids 的“中心”(medoid)必须是数据集里的一个真实点。所以 k-medoids 对离群点(奇怪的朋友)更不敏感,更符合适合现实中的情况。
举个例子:
假设你发了一个问卷,收集了很多人在「幸福感」上的评分,维度包括:
- 工作满意度
- 家庭支持度
- 自我成长评分
- 社交活跃度
你想把人群分成几种幸福感类型。
K-Means 得到的中心是所有维度的“平均值”,可能是一个看起来“中等满意、一般社交、轻度焦虑”的组合,但现实中可能没人刚好同时具备这些特点。
而 K-Medoids 会告诉你:“第 27 号填表者”就是最能代表第 1 组的人。 你可以直接点开他的完整问卷,看他是个什么样的人、怎么活的、怎么想的——真实且可解读。
这就非常适合社会科学里的一些特点,因为我们经常需要找出“代表人物”“典型样本”,比如社会群体中的“典型用户”“典型行为者”,或者在心理访谈中选出“最能代表某类受访者”的那一位。 我们不想拿一个“平均人”来代表某个群体,我们想找一个真实存在的人,他就在这个群体里。
K-medoids是怎么做的呢?#
- 随便挑 k 个带头大哥:从数据里随机选
k个点作为初始 medoids。 - 分组:每个点去找离自己最近的 medoid,加入那个组。
- 检查谁更适合当大哥:对每个组,试试组里其他点当 medoid,看看总距离能不能变小。
- 换大哥:如果找到更合适的 medoid,就换掉原来的,继续分组。
- 停下来:如果换来换去没啥变化了(总距离不减了),就结束。
简单举个例子#
假设有 5 个点:1, 3, 10, 12, 20,我们想分成 2 组(k=2)。
- 随机选 1 和 10 当 medoids。
- 分组:1 和 3 离 1 近,10、12、20 离 10 近。
- 检查:如果把 3 换成 medoid,可能总距离更小,那就换。
- 重复,直到稳定,比如最后可能是 3 和 12 当 medoids。
再来一个例子:你想把一群人按身高聚成 3 类。
K-Means 会按平均身高来算中心点,但那可能是一个“虚拟值”,现实中没人身高正好等于它。
K-Medoids 则是选这堆人里面“最能代表这个群体的人”来当中心点。
- K-Means 选的是“平均值点(中心点)”
- K-Medoids 选的是“实际数据点里最合适的点(代表点)”
- 所以 K-Medoids 对“离群点(outlier)”更不敏感,结果更稳定。
K-Medoids 适用场景#
1. 数据中存在离群值或异常点#
K-Medoids 不容易被极端值“拉偏”,因为它选的中心点是数据集中实际存在的点,而不是被少数极端值“拉”出来的平均值。
举个例子:
在一组用户收入的数据中,大部分人月收入 3k–8k,但有个超级富豪月入 100w。
- K-Means 可能把中心点拉向富豪那边,造成结果整体偏移;
- K-Medoids 依然会选一个普通人作为中心,因为富豪只是个“异类”,不会被选为代表。
适合场景:
- 社会科学调研中经常出现“特殊人群”
- 医疗数据中存在异常指标(例如某个患者血压非常高)
2. 希望中心点是某个真实存在的样本点#
K-Medoids 的中心(medoid)必须是某一个真实存在的数据点,所以我们能:
- 点名找到它,查看它的原始信息;
- 用它作为个案代表;
- 进行“典型用户”分析、抽样调查、个体访谈等。
这对于商业场景、社会科学、用户研究特别重要,因为我们不想要一个虚构的代表,我们要一个能看见、能理解、能联系的真实人。
3. 距离计算不一定是欧氏距离#
K-Means 默认使用欧氏距离(空间上的直线距离),这要求数据必须是数值型、可以进行“平均”。
K-Medoids 更灵活——只要你能定义“相似度”或“距离”,它都能用。
举例:
- 文本之间用“编辑距离”或“Jaccard 距离”
- 用户行为序列之间用“Optimal Matching(最有匹配)”或者“DTW(动态时间规整)”
- 图像、基因、网络节点之间的“自定义距离”
适合场景:
- 文本聚类(邮件分类、新闻聚合)
- 基因序列聚类
- 用户轨迹/点击序列聚类
4. 聚类结果需要可解释性、可操作性#
有些行业不只是要聚完类,还要:
- 向客户汇报:“这是谁代表的?”
- 给业务团队建议:“我们应该关注哪一类人?”
- 给 AI 模型标注:“选哪几个点做人工审核?”
K-Medoids 给出的“中心”点是实际样本,天然具有可解释性。
适合场景:
- 金融风控、社交平台治理、政府政策制定等场景下,需要对“聚类结果”有明确交代。
总结:K-Medoids 更适合这些情况#
| 场景类型 | 描述 |
|---|---|
| 存在极端值或异常点 | 数据中包含离群样本(不一定是“错误”),希望聚类结果对它们更稳健 |
| 要找代表样本 | 希望选出真实的代表用户 / 病人 / 问卷对象 |
| 距离无法平均 | 文本、符号序列、结构化数据不能求均值 |
| 解释性要求高 | 聚类结果需要被“看懂、讲明白、执行” |
| 商业场景/社会经济/人文 | 不只是分类,更关注真实案例,便于决策落地 |
关键概念的中英文对照:#
| 概念 | 中文解释 | 英文术语 |
|---|---|---|
| Medoid | 中心点(真实数据点) | Medoid |
| Clustering | 聚类 | Clustering |
| Inertia / Cost | 聚类代价 | Total Cost |
| Distance | 距离(如曼哈顿/欧几里得) | Distance Function |
K-Medoids 的算法流程#
还记得我们上面写的“带头大哥”案例吗?我们再给大家讲解一下严肃版本的算法流程:
- 选择 k 个数据点作为初始中心(称为 medoids,也就是中心点/中位点)
- 将每个样本分配给最近的中心点
- 尝试将某个中心点和某个非中心点交换,如果交换后总距离变小,就保留
- 重复 2-3,直到没有更优的交换为止
咱们用可视化的方式帮助你来理解:
pip install scikit-learn matplotlib scikit-learn-extraimport numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets import make_blobsfrom sklearn.cluster import KMeansfrom sklearn_extra.cluster import KMedoidsfrom sklearn.metrics import pairwise_distances_argmin_min
# 生成主簇 + 多个离群点X, _ = make_blobs(n_samples=300, centers=3, cluster_std=0.9, random_state=42)outliers = np.random.uniform(low=15, high=25, size=(30, 2))X_with_outliers = np.vstack([X, outliers])
# KMeanskmeans = KMeans(n_clusters=3, random_state=42).fit(X_with_outliers)kmeans_labels = kmeans.labels_kmeans_centers = kmeans.cluster_centers_
# KMedoidskmedoids = KMedoids(n_clusters=3, method='alternate', random_state=42).fit(X_with_outliers)kmedoids_labels = kmedoids.labels_kmedoids_centers = kmedoids.cluster_centers_
# 标签颜色对齐mapping = pairwise_distances_argmin_min(kmedoids_centers, kmeans_centers)[0]aligned_kmedoids_labels = np.array([mapping[label] for label in kmedoids_labels])
# 可视化(美观版)fig, axes = plt.subplots(1, 2, figsize=(14, 6))titles = ['K-Means 聚类(受异常点影响)', 'K-Medoids 聚类(更稳健)']colors = ['#1f77b4', '#ff7f0e', '#2ca02c']
for ax, labels, centers, title, marker, center_color in zip( axes, [kmeans_labels, aligned_kmedoids_labels], [kmeans_centers, kmedoids_centers], titles, ['X', 'D'], ['red', 'blue']): for i in range(3): cluster_points = X_with_outliers[labels == i] ax.scatter(cluster_points[:, 0], cluster_points[:, 1], s=30, color=colors[i], alpha=0.7) ax.scatter(centers[:, 0], centers[:, 1], c=center_color, marker=marker, s=250, edgecolor='white', linewidth=2, label='中心点') ax.set_title(title, fontsize=14) ax.set_xlim(-10, 30) ax.set_ylim(-10, 30) ax.grid(True, linestyle='--', alpha=0.5) ax.legend()
plt.tight_layout()plt.show()上面代码得出来的这张图非常适合用来讲解 K-Means 和 K-Medoids 在面对“疑似新簇”时的差异与策略选择。
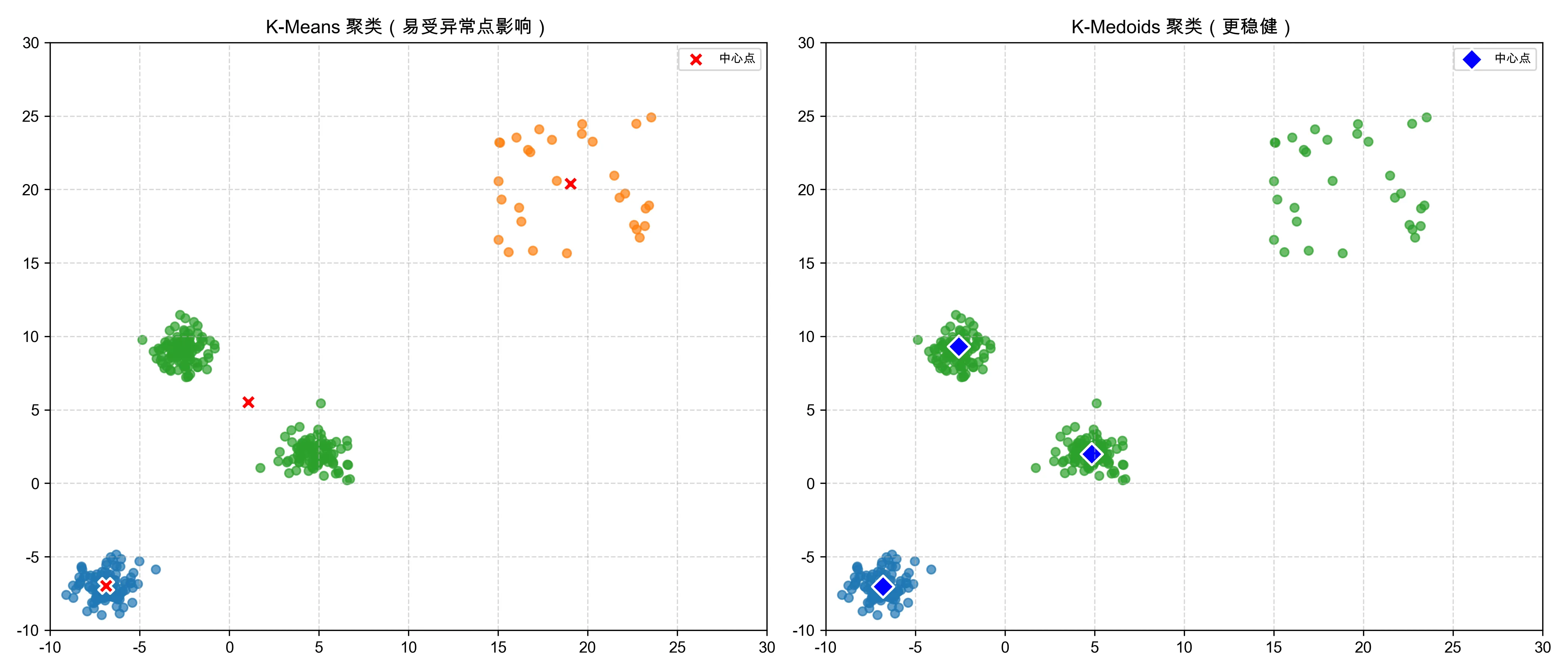
左图:K-Means 聚类(受异常点影响?还是发现新簇?)#
- 红色叉叉
✖是 K-Means 算法计算出来的中心点(不是原始数据中的点,而是“平均值”) - 你可以看到,右上角那些点被归为一个独立簇(橙色),并且 K-Means 为它计算了一个中心
- 乍一看,这些点是我们人为加的“离群点”,但它们集中且数量不少,所以 K-Means 合理地把它们识别成一个新簇
- 优点:灵敏、可以自动发现潜在结构
- 风险:当这些点是异常数据时,反而可能“误识别”它们为真正的模式
右图:K-Medoids 聚类(稳健保守,不轻易接纳新簇)#
- 蓝色菱形
◆是 K-Medoids 算法选出来的中位点(真实存在于数据中的点) - K-Medoids 并没有承认右上角那些点是一个新簇
- 它依然只认定了原始三个主簇,并用真实样本来代表每个中心
- 这些右上角的点(虽然聚得挺紧)被分配到了离它们最近的真实中心
- 造成了这些点在聚类结果中“没有自己的家”
- 优点:抗异常点干扰,不轻易误判
- 风险:对新出现的小簇不够敏感,可能漏掉一些潜在结构
但你可能会问:
“但是这些离群点感觉也像是一个簇啊?”
这体现出一个很重要的思想:
- 聚类没有“绝对正确”,取决于你怎么看这些数据:
- 如果你认为这些右上角的点是异常值 → K-Medoids 更合适
- 如果你认为这些点是新出现的一类结构 → K-Means 发现了它
这也意味着,K-Means 和 K-Medoids 的“差异”不是孰优孰劣,而是取舍不同;简单来说,两个算法里面,一个比较激进,一个比较保守。
小结:图中的观察#
| 对比维度 | K-Means | K-Medoids |
|---|---|---|
| 对右上角点的处理 | 成为新簇 | 被归到其他簇 |
| 中心点位置 | 可能被异常点拉偏 | 更贴近主簇核心 |
| 是否认为“右上角是一个新簇” | 是(发现结构) | 否(认为它不够代表性) |
| 更适合何种需求 | 结构探索、发现潜在模式 | 稳健聚类、抗噪音任务 |
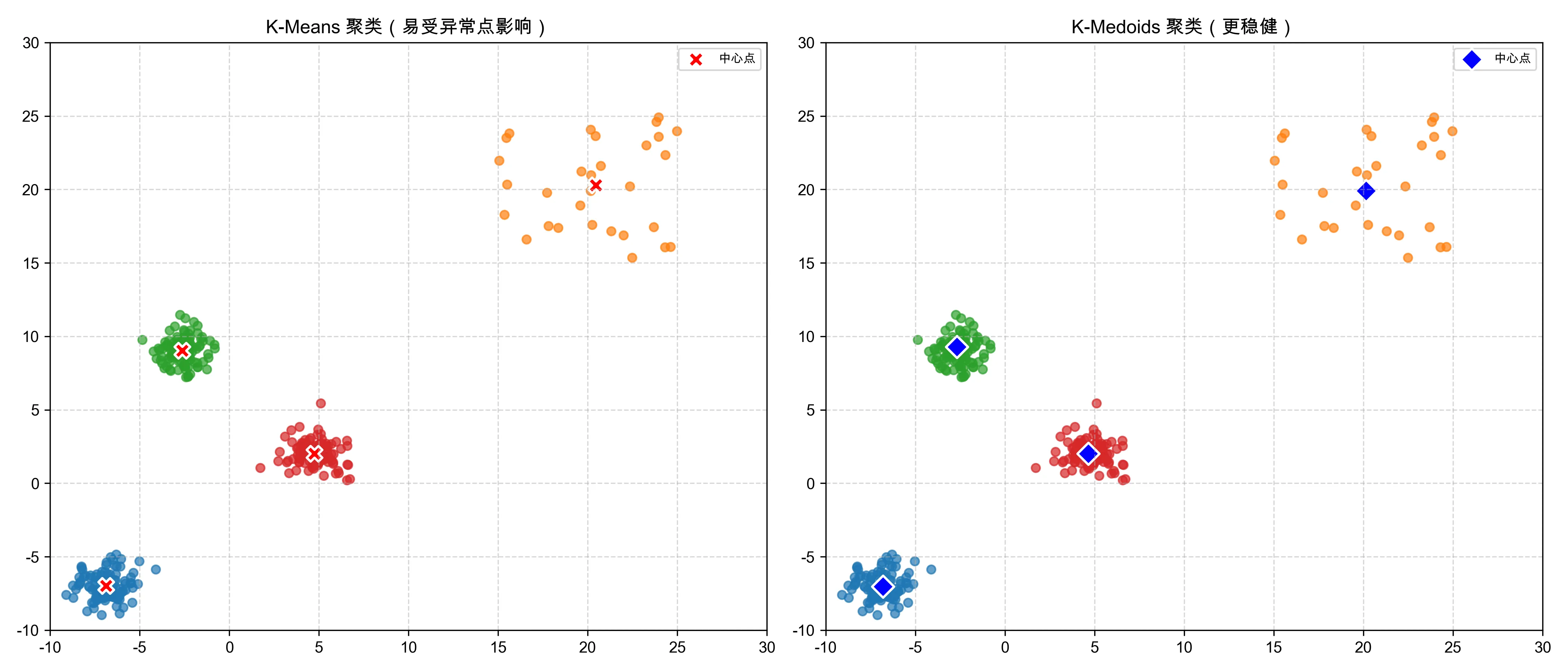
下面是4个聚类的结果,可以看到这里就没有3个聚类的时候有争议性了,因为 K-Means 和 K-Medoids 都有了一致的聚类结果:
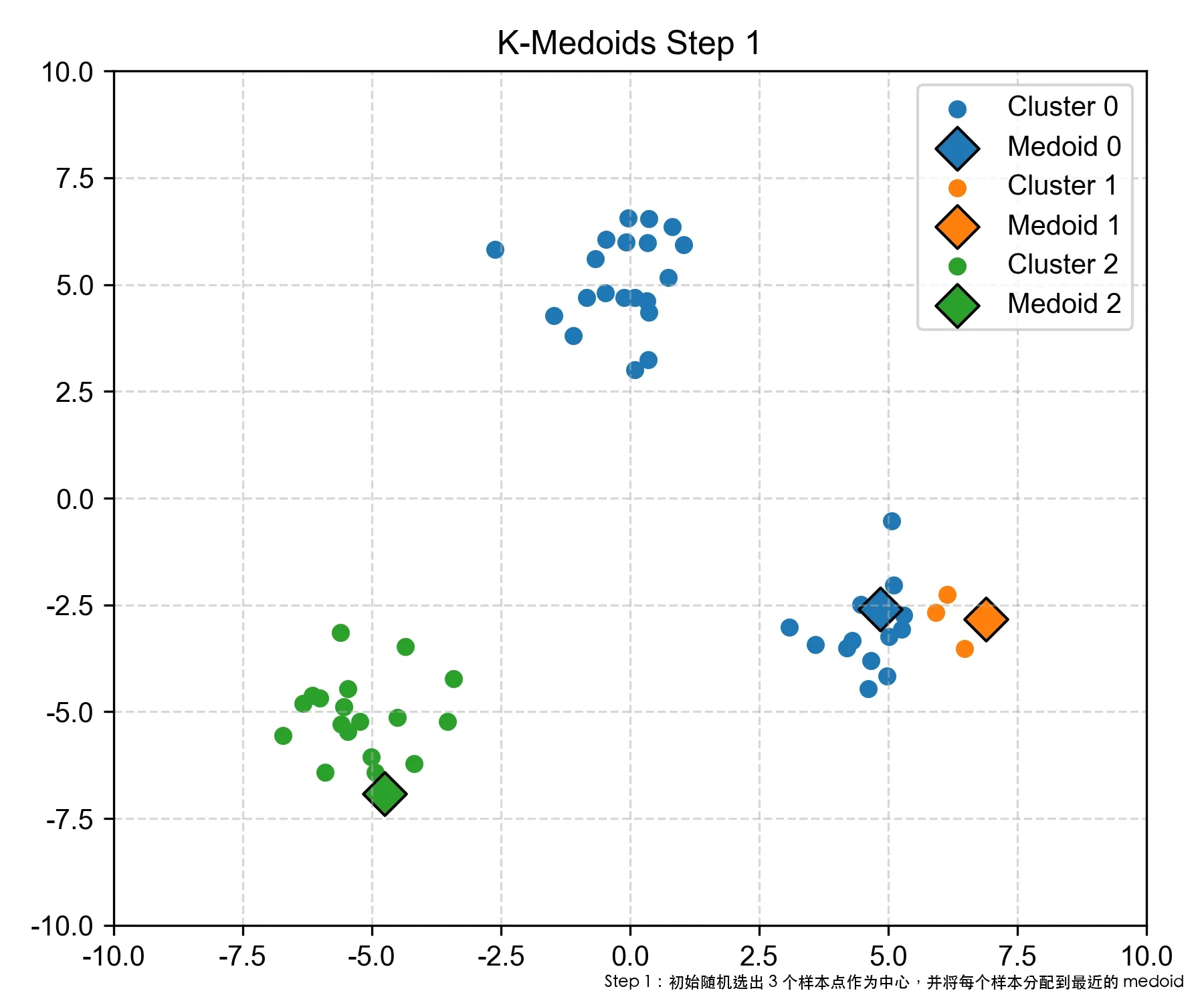
K-Medoids 聚类演化过程图#
下面是我做的一个 gif 动态图,帮助大家理解这个算法一步一步到底怎么做的。图的右下角有这个 gif 在你阅读的当前到底经历到了哪一步,如果还没有到第一步,就可以等一等,然后从第一步开始看。
我们接下来就来一张张详细解释这6个步骤,用非常通俗的方式帮助你理解这个算法的核心思想。
Step 1:初始随机选出 3 个样本点作为中心,并将每个样本分配到最近的 medoid#
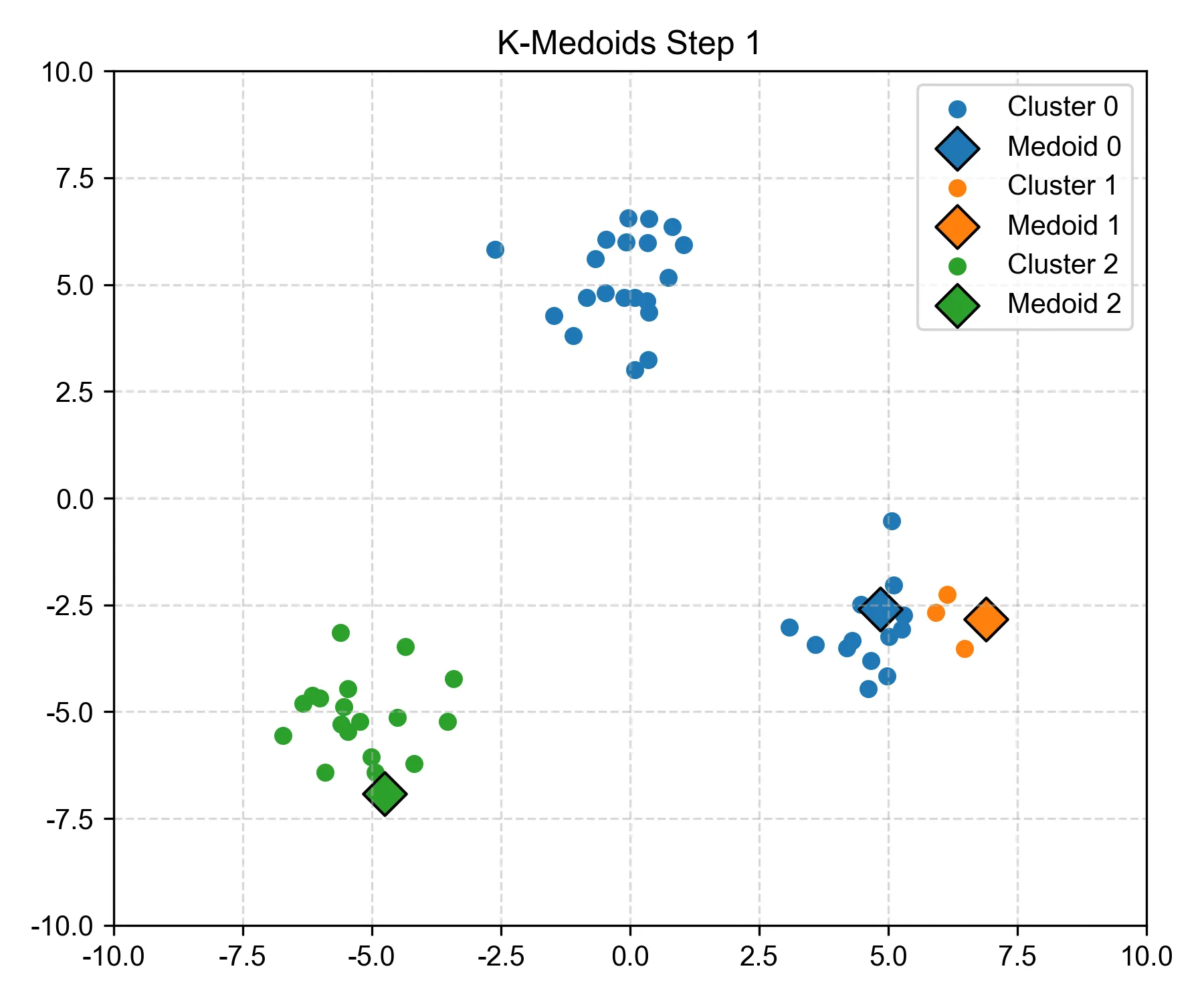
- 图中大菱形的点,就是初始的 “medoids”。
- 我们不像 K-Means 那样平均取点,而是直接从原始数据中挑 3 个点出来当作初始“代表”。 这些代表点将会“竞争拉拢”周围的样本,看谁离它更近。
- 在这里,我们可以发现,随机抽取的两个中心点在右下角的这个簇里(一个绿色,一个橙色),这显然不是最优化的解,因此之后算法也会对此进行调整。
- 暂时确定了三个中心点之后,每个点都会测量:我离哪个 medoid 最近?然后就“投奔”它,成为它的成员。
- 所以你看到簇的雏形就出来了,不同颜色表示被哪个中心“招募”了。
Step 2:尝试替换某个 medoid,如果可以降低总距离则替换#
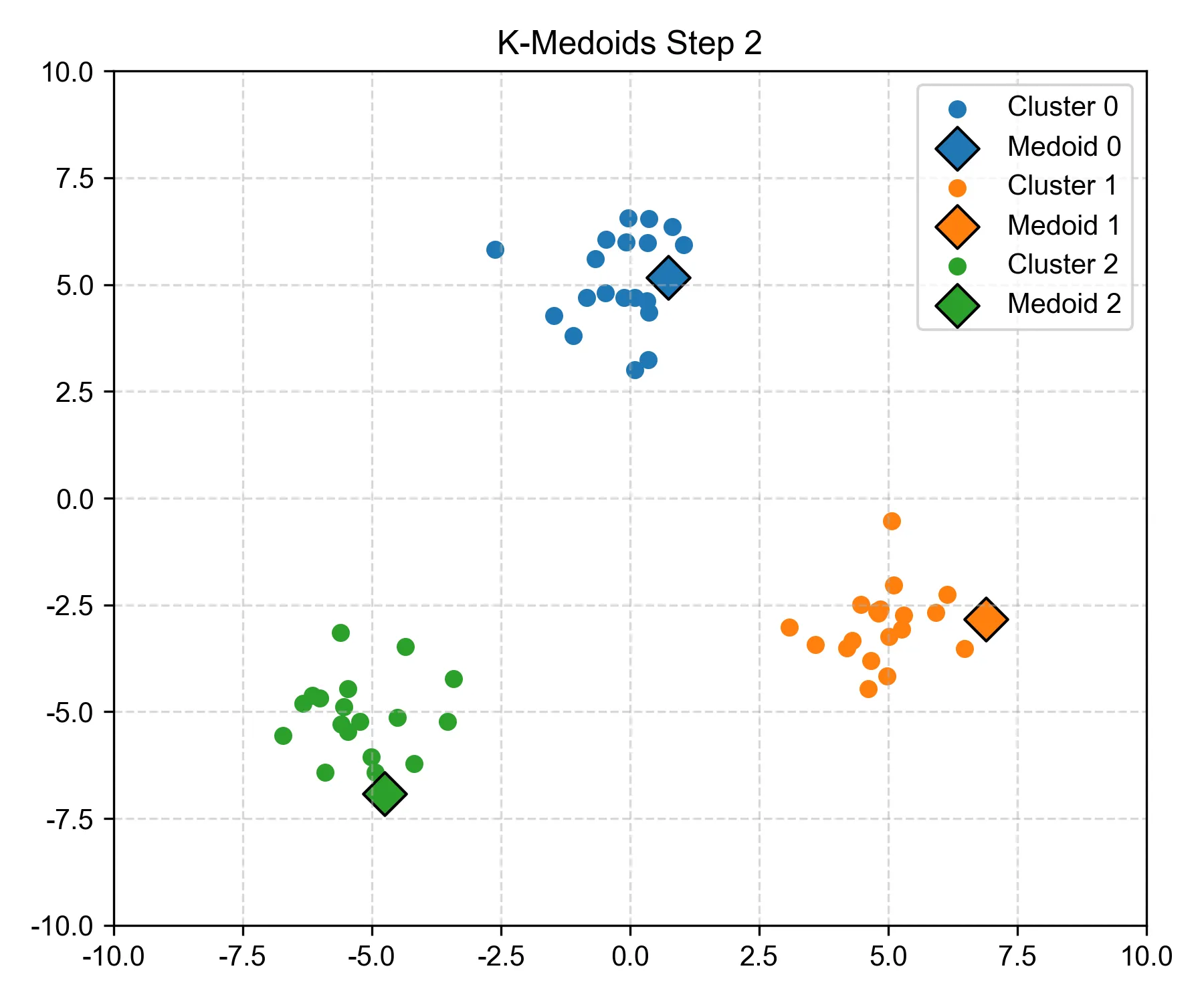
- 看起来图中蓝色的 medoid 被替换了。
- 虽然比上一个步骤的簇分类更合理了,但当前中心点不一定是最好的。
- 所以算法会尝试一个“调岗试验”:如果我们把蓝色中心换成它簇里的另一个点,会不会让大家到中心的距离更短?如果试出来效果好,就真的换掉。
Step 3:再次尝试替换某个 medoid,如果可以降低总距离则替换#
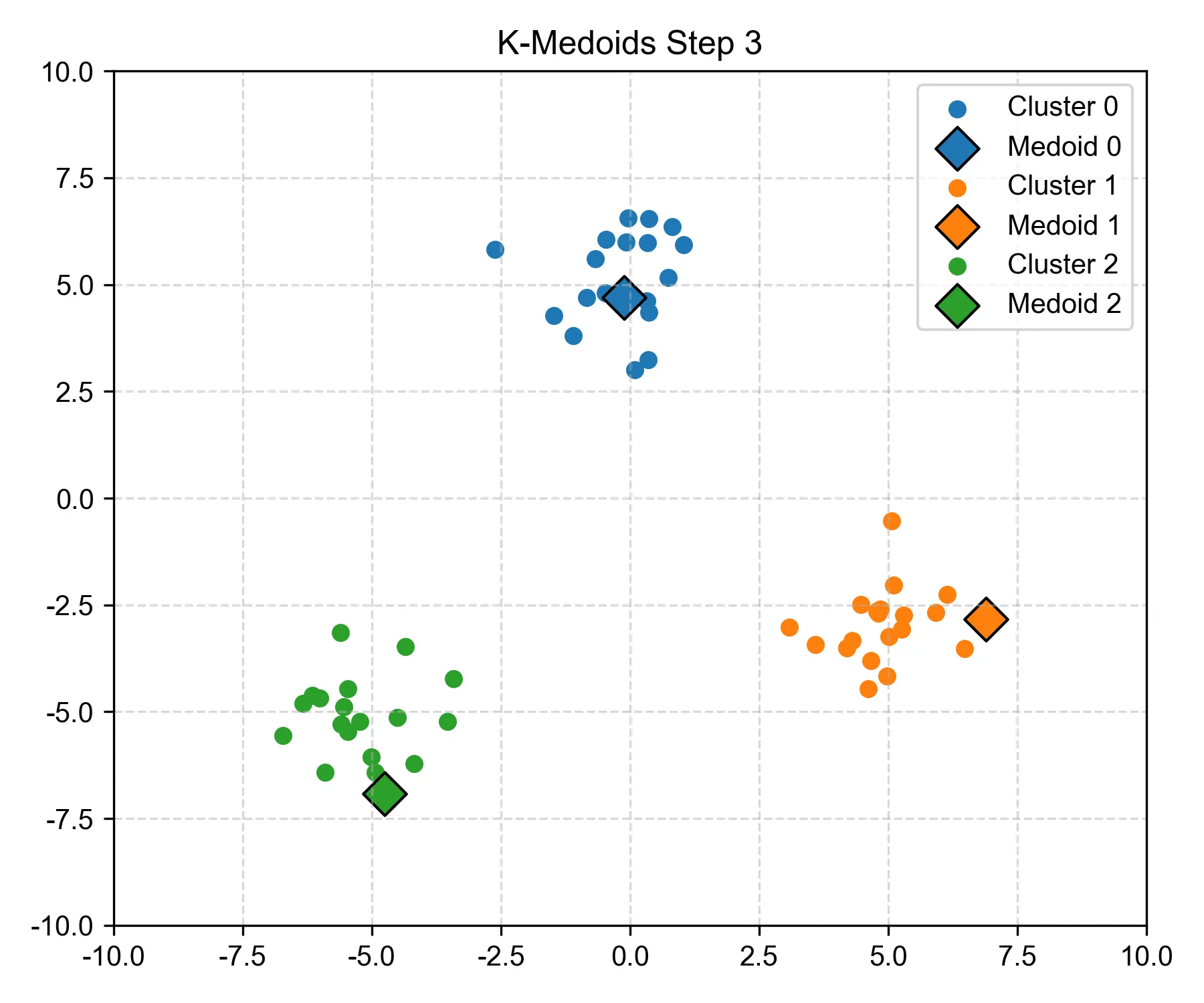
- 再次调整中心点和相应的簇,计算各个簇到中心的距离,看是否能让大家到中心的距离更短。
- 算法发现,蓝色的簇中心需要进行替换,所以最上面的簇中心有些许的改变。
Step 4:橙色簇中心发生更新,分类重新分配#
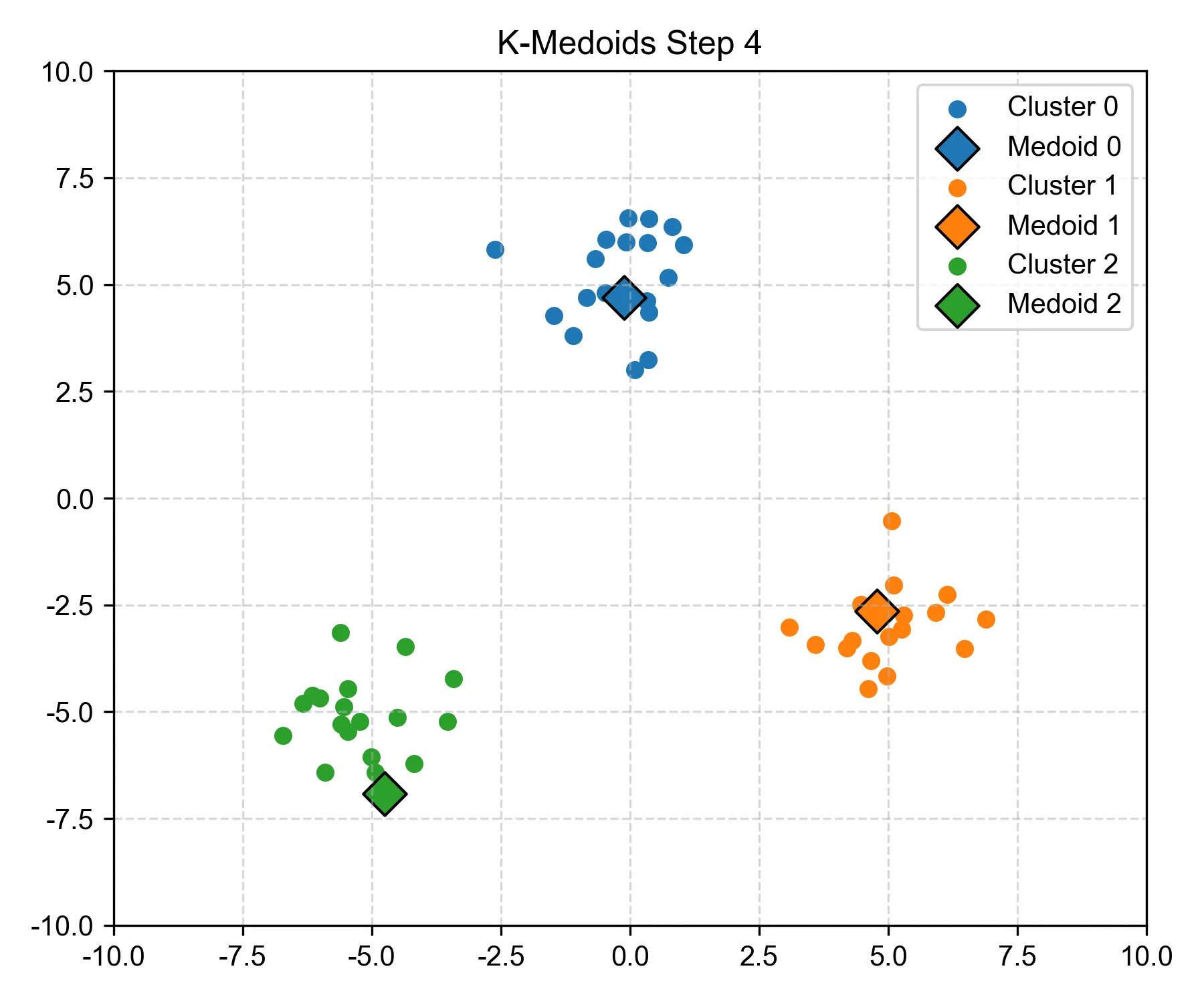
- 这一次,你会看到橙色中心点的分配发生了变化。中心点变了,自然要重新计算谁该属于谁。
- 一旦分类变了,下一轮也可能影响下一个 medoid。
- 就这样一步步修正,越来越合理。
Step 5:所有点都尝试过替换后,发现未能进一步降低成本#
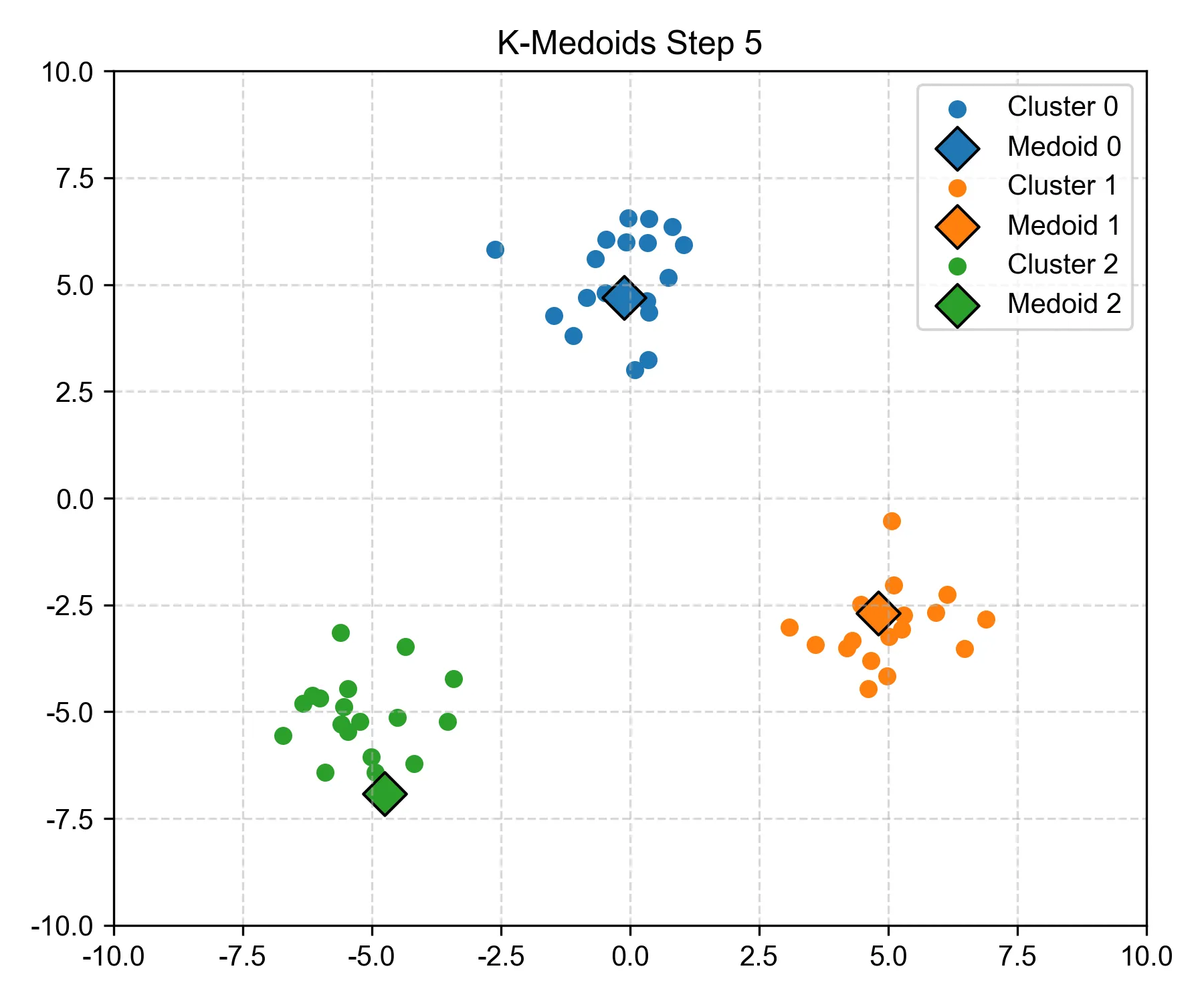
- 看似没有任何变化。
- 算法已经尝试了“换人”,但没有更优解。
- 意味着当前中心组合已经是最优或局部最优解。
Step 6:达到收敛,不再更新,聚类完成,得到最终稳定的分簇结构#
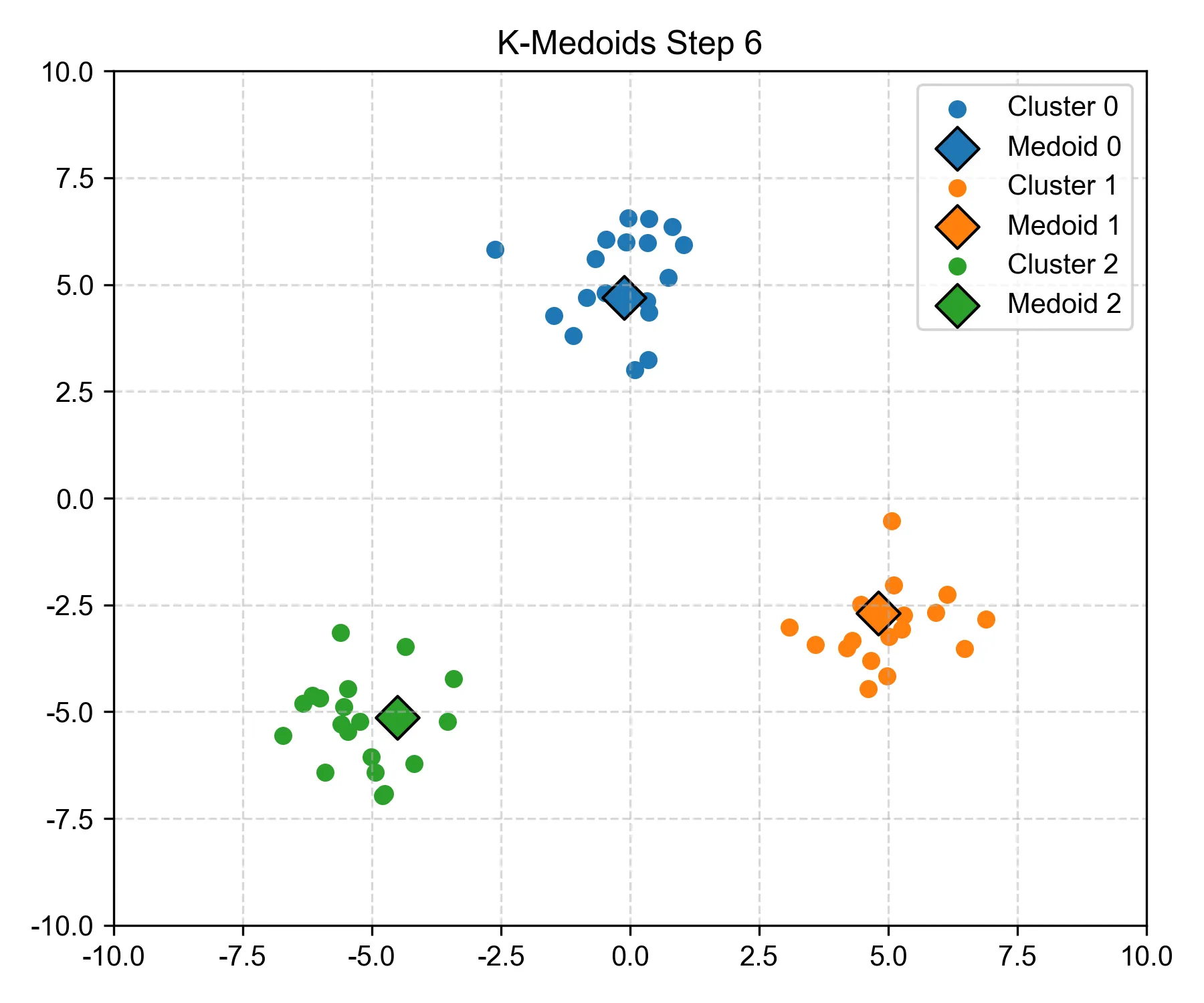
- 和 Step 5 相同,代表稳定下来。 这就是所谓的“收敛”:不换了,就这样了。
- 相比 K-Means,K-Medoids 更稳定,因为它不受极端值影响太大。
- 每个 medoid 都是簇内最具有代表性的那个点(不是平均值,而是实际存在的样本)。这使得 K-Medoids 非常适合存在异常值的情况。
- 当然,缺点也会有:计算量比 K-Means 大,但换来了更稳健的结果。
那我们再来小小地总结一下,加深理解:#
| 特点 | K-Means | K-Medoids |
|---|---|---|
| 中心点类型 | 均值(可能不是实际数据点) | 原始数据点中的某一个 |
| 抗离群点能力 | 弱,容易被拉偏 | 强,不易被极端点影响 |
| 计算速度 | 较快 | 慢一些(要试很多组合) |
对比分析 Python / C++ / Rust 三种语言中 K-Medoids 的实现#
我为什么要给大家展示这三种语言的算法版本?
- Python:用来让大家快速明白算法流程。
- C++:你可以练习边界条件处理、循环嵌套、性能思维。
- Rust:适合对内存安全、现代语言风格有兴趣的同学进阶使用。
- 帮助大家不仅读懂每种代码,还能理解它们之间的结构异同点,培养跨语言思维
Python 实现(用的是常规写法,不依赖特殊库)#
import randomimport numpy as np
def manhattan_distance(a, b): return np.sum(np.abs(a - b)) # 你也可以改成欧氏距离
def total_cost(data, medoids, clusters): cost = 0 for i, cluster in enumerate(clusters): for point in cluster: cost += manhattan_distance(data[point], data[medoids[i]]) return cost
def assign_points(data, medoids): clusters = [[] for _ in medoids] for idx, point in enumerate(data): distances = [manhattan_distance(point, data[medoid]) for medoid in medoids] min_index = np.argmin(distances) clusters[min_index].append(idx) return clusters
def k_medoids(data, k, max_iter=100): n = len(data) medoids = random.sample(range(n), k) for _ in range(max_iter): clusters = assign_points(data, medoids) best_cost = total_cost(data, medoids, clusters) changed = False
for i in range(k): for j in range(n): if j in medoids: continue new_medoids = medoids[:] new_medoids[i] = j new_clusters = assign_points(data, new_medoids) new_cost = total_cost(data, new_medoids, new_clusters) if new_cost < best_cost: medoids = new_medoids best_cost = new_cost changed = True if not changed: break return medoids, assign_points(data, medoids)C++ 实现(简化版,目前的版本适合小数据)#
注意:当前的版本更适合刚开始学习使用,当同学熟悉之后,可以看看 R 包 WeightedCluster 对 K-Medoids 的版本对照
#include <iostream>#include <vector>#include <cstdlib>#include <ctime>#include <cmath>#include <limits>using namespace std;
double distance(const vector<double>& a, const vector<double>& b) { double sum = 0; for (size_t i = 0; i < a.size(); i++) sum += abs(a[i] - b[i]); return sum;}
double total_cost(const vector<vector<double>>& data, const vector<int>& medoids, const vector<vector<int>>& clusters) { double cost = 0; for (size_t i = 0; i < clusters.size(); i++) for (int idx : clusters[i]) cost += distance(data[idx], data[medoids[i]]); return cost;}
vector<vector<int>> assign(const vector<vector<double>>& data, const vector<int>& medoids) { vector<vector<int>> clusters(medoids.size()); for (int i = 0; i < data.size(); i++) { double min_dist = numeric_limits<double>::max(); int best = 0; for (int j = 0; j < medoids.size(); j++) { double d = distance(data[i], data[medoids[j]]); if (d < min_dist) { min_dist = d; best = j; } } clusters[best].push_back(i); } return clusters;}
pair<vector<int>, vector<vector<int>>> k_medoids(const vector<vector<double>>& data, int k) { srand(time(0)); int n = data.size(); vector<int> medoids; while (medoids.size() < k) { int r = rand() % n; if (find(medoids.begin(), medoids.end(), r) == medoids.end()) medoids.push_back(r); }
for (int iter = 0; iter < 100; iter++) { auto clusters = assign(data, medoids); double best_cost = total_cost(data, medoids, clusters); bool changed = false;
for (int i = 0; i < k; i++) { for (int j = 0; j < n; j++) { if (find(medoids.begin(), medoids.end(), j) != medoids.end()) continue; vector<int> new_medoids = medoids; new_medoids[i] = j; auto new_clusters = assign(data, new_medoids); double new_cost = total_cost(data, new_medoids, new_clusters); if (new_cost < best_cost) { medoids = new_medoids; best_cost = new_cost; changed = true; } } } if (!changed) break; }
return {medoids, assign(data, medoids)};}Rust 实现(简洁版)#
use rand::seq::SliceRandom;use rand::thread_rng;
fn manhattan(a: &[f64], b: &[f64]) -> f64 { a.iter().zip(b).map(|(x, y)| (x - y).abs()).sum()}
fn assign(data: &[Vec<f64>], medoids: &[usize]) -> Vec<Vec<usize>> { let mut clusters = vec![vec![]; medoids.len()]; for (i, point) in data.iter().enumerate() { let (min_idx, _) = medoids.iter() .enumerate() .map(|(j, &m)| (j, manhattan(point, &data[m]))) .min_by(|a, b| a.1.partial_cmp(&b.1).unwrap()) .unwrap(); clusters[min_idx].push(i); } clusters}
fn total_cost(data: &[Vec<f64>], medoids: &[usize], clusters: &[Vec<usize>]) -> f64 { clusters.iter().enumerate().map(|(i, cluster)| { cluster.iter().map(|&j| manhattan(&data[j], &data[medoids[i]])).sum::<f64>() }).sum()}
fn k_medoids(data: &[Vec<f64>], k: usize) -> (Vec<usize>, Vec<Vec<usize>>) { let mut rng = thread_rng(); let mut medoids: Vec<usize> = (0..data.len()).collect(); medoids.shuffle(&mut rng); medoids.truncate(k);
for _ in 0..100 { let clusters = assign(data, &medoids); let mut best_cost = total_cost(data, &medoids, &clusters); let mut updated = false;
for i in 0..k { for j in 0..data.len() { if medoids.contains(&j) { continue; } let mut new_medoids = medoids.clone(); new_medoids[i] = j; let new_clusters = assign(data, &new_medoids); let new_cost = total_cost(data, &new_medoids, &new_clusters); if new_cost < best_cost { medoids = new_medoids; best_cost = new_cost; updated = true; } } }
if !updated { break; } }
(medoids, assign(data, &medoids))}具体理解#
我们要实现的都是同一个目标:
给定一堆数据点,找出
k个代表(medoids),把所有点分进离它们最近的“带头大哥”。
核心步骤回顾(所有语言都一样):
- 初始化:随机选出
k个点作为初始 medoids。 - 分配点:每个点分到离它最近的 medoid 所在的簇。
- 优化 medoid:尝试替换 medoid,若总距离变小,就更新。
- 重复:直到收敛(不再更新)。
Python 版本的要点解析:最容易读懂,结构清晰,语法简洁#
def manhattan_distance(a, b): return np.sum(np.abs(a - b))使用曼哈顿距离(当然也可以改成欧氏距离),这样计算两个向量之间的距离。在社会序列分析中,一般使用的是其他dissimilarity measures,比如 optimal matching(最优匹配)。
def assign_points(data, medoids): clusters = [[] for _ in medoids] ...assign_points() 函数会把每个点分配给最近的 medoid,并组成簇。
for i in range(k): for j in range(n): if j in medoids: continue尝试将一个新的点替换当前的 medoid,判断是否更优。
C++ 版本的要点解析:需要注意更底层的东西#
- 适合练习数据结构 / 指针理解
- 逻辑和 Python 接近,但需要自己控制内存结构
vector是核心数据结构
double distance(const vector<double>& a, const vector<double>& b)使用 abs 实现曼哈顿距离。这里用的是 double,没有模板泛型,简单粗暴。
vector<vector<int>> assign(const vector<vector<double>>& data, const vector<int>& medoids)和 Python 一样,遍历每个数据点,把它放进最近的 medoid 所属的簇。
for (int i = 0; i < k; i++) { for (int j = 0; j < n; j++) { ...嵌套遍历:尝试替换某个 medoid,看看有没有更好的聚类结构(距离更小)。
Rust 版本的要点解析:安全强大,但稍微晦涩难懂(刚开始学习的曲线比较陡峭)#
- 类型安全、无空指针崩溃
- 所有权系统防止内存泄露
- 代码结构更“函数式”
fn manhattan(a: &[f64], b: &[f64]) -> f64 { a.iter().zip(b).map(|(x, y)| (x - y).abs()).sum()}Rust 没有 numpy 之类的工具包,得用迭代器组合:zip → map → sum。
fn assign(data: &[Vec<f64>], medoids: &[usize]) -> Vec<Vec<usize>> { ... }用 Vec<Vec<usize>> 表示所有簇,每个簇中是原始数据点的索引(和 Python 一致)。
medoids.shuffle(&mut rng);medoids.truncate(k);shuffle + truncate 是 Rust 的随机初始化方式(类似 Python 的 random.sample)。
总结:三语言结构对照总结表#
| 功能 | Python | C++ | Rust |
|---|---|---|---|
| 数据结构 | list, numpy | vector | Vec, slice |
| 随机初始化 | random.sample() | rand() % n | shuffle + truncate |
| 距离函数 | np.abs(a - b).sum() | abs(a[i] - b[i]) | zip().map().sum() |
| 聚类表示 | List[List[int]] | vector<vector<int>> | Vec<Vec<usize>> |
| 替换逻辑 | for i in range(k) | for (int i = 0; i < k) | for i in 0..k |
| 是否收敛 | if not changed: break | if (!changed) break; | if !updated { break; } |
| 总体写法风格 | 简洁、解释性强 | 稍长但结构清晰 | 类型安全但语法偏函数式 |
思考题(也很重要,加深理解)#
- 如果我们用欧氏距离(Euclidean),各语言代码应该怎么改?
- 如何避免暴力搜索(加速 medoid 替换)?
- Rust 中如果不想复制
Vec,有没有更高效写法?
思考题解析#
1. 如果我们用欧氏距离 (Euclidean),各语言代码应该怎么改?#
欧氏距离公式:
distance(a, b) = √((a1 - b1)² + (a2 - b2)² + ...)但 K-Medoids 只求 距离大小比较,不需要真的开方,所以 可省略 sqrt 提升性能。
-
Python:
# 替换 manhattan_distance 内容np.sum((a - b) ** 2) # 不加 sqrt 更快# 如果坚持开方np.sqrt(np.sum((a - b) ** 2)) -
C++:
double distance(const vector<double>& a, const vector<double>& b) {double sum = 0;for (size_t i = 0; i < a.size(); i++)sum += pow(a[i] - b[i], 2);return sqrt(sum); // 可省略} -
Rust:
fn euclidean(a: &[f64], b: &[f64]) -> f64 {a.iter().zip(b).map(|(x, y)| (x - y).powi(2)).sum::<f64>().sqrt()}或省略开方:
a.iter().zip(b).map(|(x, y)| (x - y).powi(2)).sum()
2. 如何避免暴力搜索?(加速 medoid 替换)#
-
每轮都要尝试将每个 medoid 替换成所有非 medoid 的点,并重新计算总距离,以寻找更优的组合,这种“枚举所有替换方案”的方式计算量很大。
具体什么意思呢?K-Medoids 算法每一步都在问: “有没有比当前这个 medoid 更合适的人选?”
于是它要做的事就是:
- 对于每个当前的 medoid(比如你选了 3 个中心) ,尝试把它换成数据集里其他所有不是 medoid 的点(比如剩下的 997 个)
- 每换一次,就重新计算一次所有样本的归属和总距离
- 如果某个替换让聚类效果更好(总距离变小),那就真的换掉
这就相当于:
- 对每个中心(medoid),你都要把所有不是中心的点试一遍
- 每试一遍,都要重算一轮“分组+代价”
所以,这是一种暴力搜索(brute-force search),尝试了所有可能的替代方案。这会导致上千次“全量重算”,代价非常大。
那么,我们该如何解决大数据 K-Medoids 性能问题?
- 预先计算 全局距离矩阵,避免重复计算
- 使用 FastPAM / CLARA / CLARANS 等改进版:
- FastPAM: 分析最可能有效的点(有一个叫做 kmedoids 的 Python 包已经对此进行了实现,详情可以点击这个链接)
- CLARA: 集合抽样
- CLARANS: 随机搜索最佳替换
- Mini-batch: 随机小数据进行替换
- 如果是在做社会序列分析的同学,可以具体分析 WeightedCluster 的代码,看看它是如何做到更快更高效的。
3. Rust 如果不想 clone Vec,有比较高效的写法吗?#
有的,Rust 重视安全和性能,但 clone 有性能损耗,我们可以进行优化。
方法 1: swap 替换 + 恢复
let old = medoids[i];medoids[i] = j; // 替换...medoids[i] = old; // 还原,避免 clone方法 2: 先记录成本,最后一次性替换
用临时变量记录最佳方案,减少内部 mut 操作。
方法 3: 小型 arrayvec 替代 Vec
use arrayvec::ArrayVec; // 限定容量,避免 heap 分配let mut medoids: ArrayVec<usize, 10> = (0..n).collect();总结对比
| 问题 | 解决方案 |
|---|---|
| 欧氏距离 | 改成平方和求和,必要时加开方 |
| 替换性能 | 预算距离 + FastPAM / CLARA |
| Rust clone | swap + 还原 / 先算后替 / 小型 ArrayVec |