在当代社会研究中,个体生命轨迹愈发呈现出多样化与非线性的特征:人们的教育路径不再单一,职业经历频繁变动,婚育模式也更加多元。
在这一背景下,如何量化这种轨迹的复杂性与多样性?
信息熵作为衡量“不确定性”的核心指标,提供了一种简洁而有力的解决方案。
本系列文章将围绕“信息熵在社会序列分析中的应用”展开,结合实际示例,从通用熵的基本概念,到横截面熵、纵向熵、局部熵,再到综合指标与实战案例,系统讲解如何用熵来刻画个体路径、群体差异和社会变迁。
在信息熵的前几期探讨中,我们系统梳理了其理论基础、计算逻辑与在社会科学中的意义。本篇作为系列的收官之作,将目光投向实证应用:如何通过不同类型的熵指标,从微观的个体生命轨迹中读出宏观的社会变迁?如何将抽象的“复杂性”量化为可比较的数值指标,并据此观察社会流动性、职业路径多样性与标准化趋势的历史演变?
为了直观演示熵分析的力量,我们以模拟数据为例,重建1950年代至1990年代出生人群的职业轨迹,分别计算并可视化横截面熵、纵向熵与局部熵。尽管数据是虚构的,但指标逻辑与解释框架均基于真实研究场景。通过这些熵指标的趋势变化,我们得以从时间和结构两个维度,洞察社会结构“去标准化”的动态过程,揭示背后深层的制度与观念转型。
本篇不仅是一次方法实操演练,更是对前文理论内容的汇总与再阐释:信息熵,如何在定量研究中扮演描述性、解释性与比较性的三重角色。
数据背景#
我们分析1950-1990年代出生人群的职业轨迹,通过三种熵指标揭示社会变迁的深层动态。由于目前缺乏这样的数据,我们在这里暂且对数据进行模拟。
熵指标综合分析#
import numpy as npimport matplotlib.pyplot as plt
# 横截面熵数据和可视化# 反映特定时间点的状态分布多样性# 从0.40上升到0.60,表明同一时间点的职业状态分布越来越多元# 社会流动性增加,职业选择更加开放cross_sectional_data = { 'cohort': ['1950s', '1960s', '1970s', '1980s', '1990s'], 'cross_sectional_entropy': [0.40, 0.45, 0.50, 0.55, 0.60]}
def plot_cross_sectional_entropy(data): plt.figure(figsize=(10, 6)) plt.bar(data['cohort'], data['cross_sectional_entropy'], color='#7eb0d5') plt.title('Cross-Sectional Entropy Across Cohorts', fontsize=16) plt.xlabel('Birth Cohort', fontsize=14) plt.ylabel('Cross-Sectional Entropy', fontsize=14) plt.ylim(0, 1) plt.show()
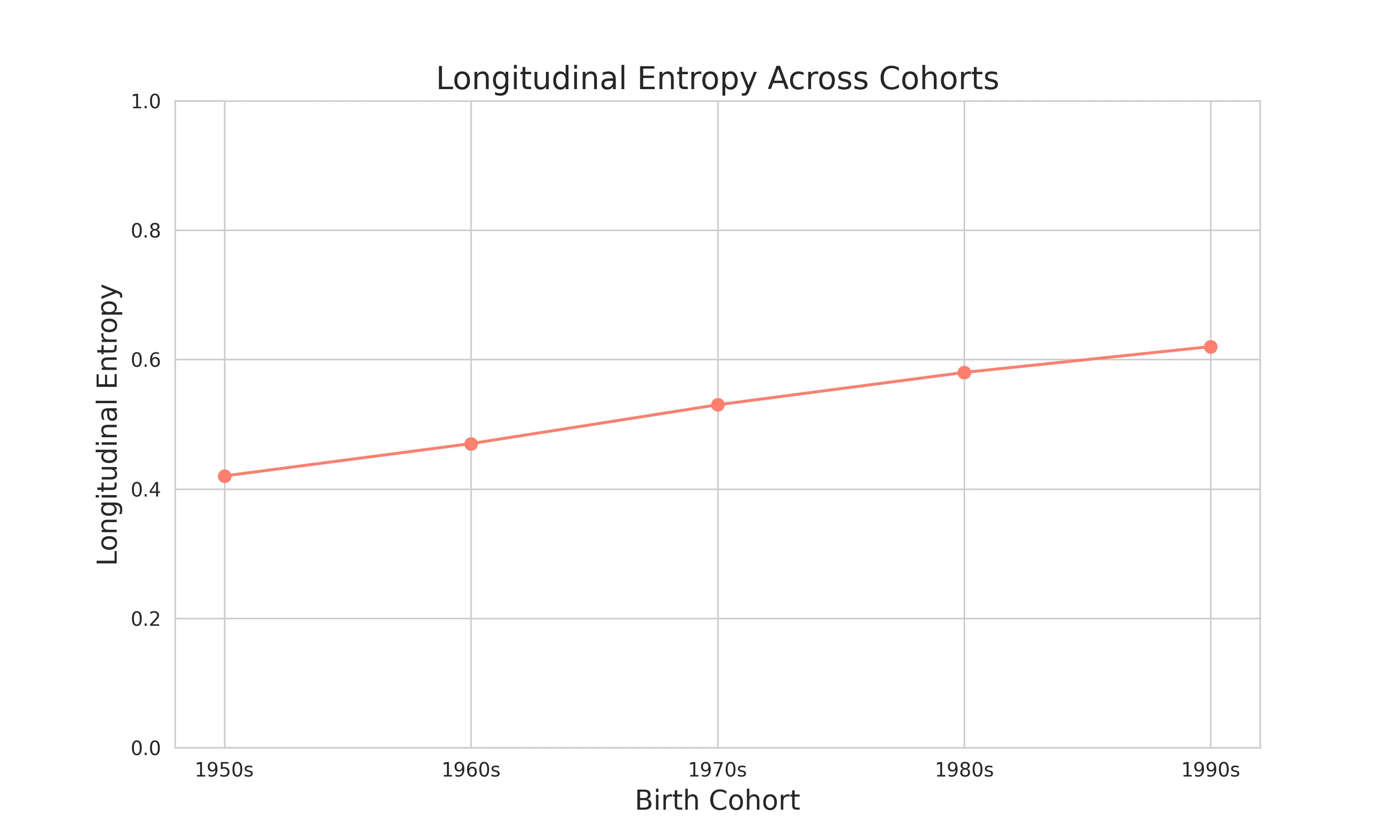
# 纵向熵数据和可视化# 揭示个人生命历程的复杂性# 从0.42稳步上升到0.62# 个人职业轨迹越来越不可预测# 生命路径变得更加多样和非线性longitudinal_data = { 'cohort': ['1950s', '1960s', '1970s', '1980s', '1990s'], 'longitudinal_entropy': [0.42, 0.47, 0.53, 0.58, 0.62]}
def plot_longitudinal_entropy(data): plt.figure(figsize=(10, 6)) plt.plot(data['cohort'], data['longitudinal_entropy'], marker='o', color='#fd7f6f') plt.title('Longitudinal Entropy Across Cohorts', fontsize=16) plt.xlabel('Birth Cohort', fontsize=14) plt.ylabel('Longitudinal Entropy', fontsize=14) plt.ylim(0, 1) plt.show()
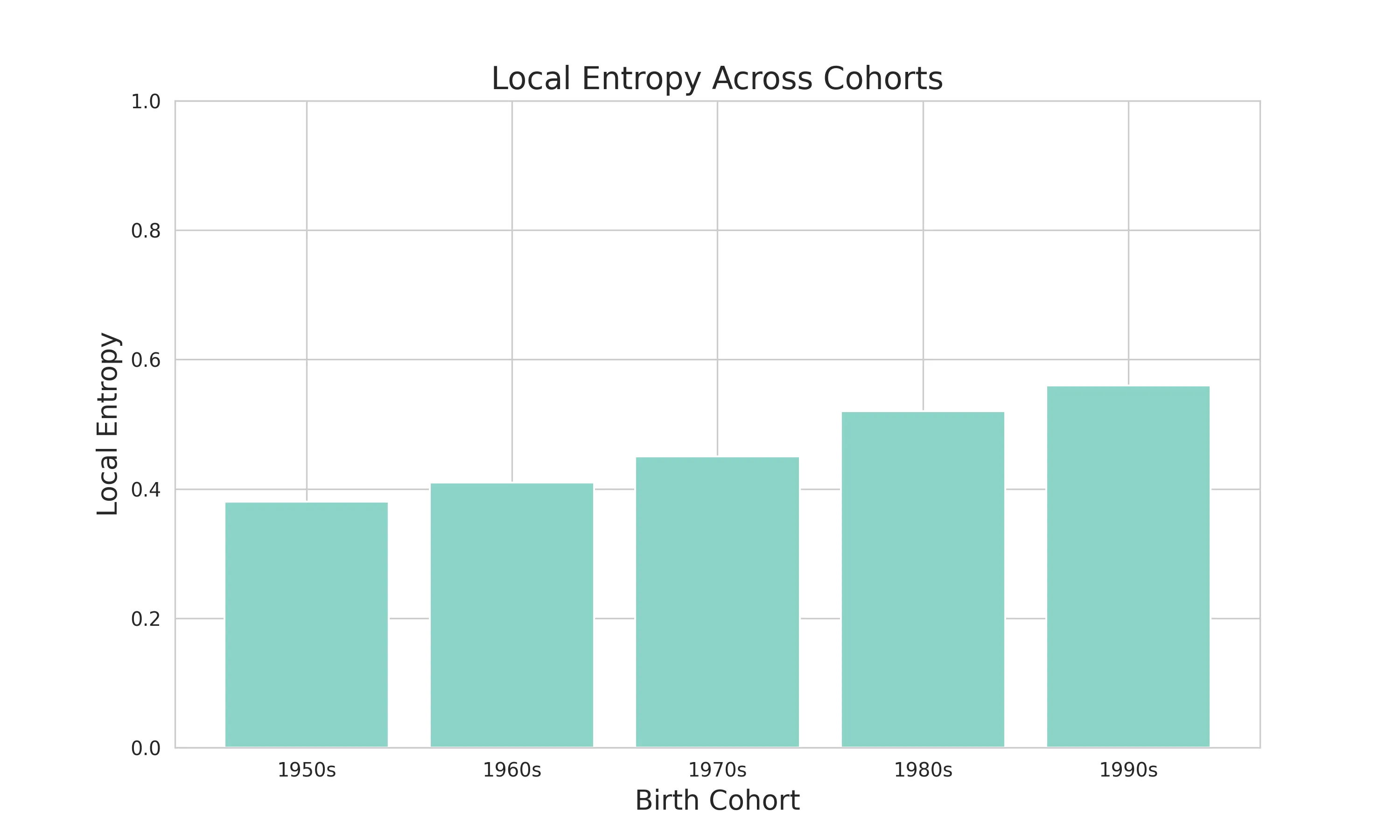
# 局部熵数据和可视化# 反映生命历程中关键转折期的不确定性# 从0.38上升到0.56# 生命重要阶段的状态变化越来越复杂# 关键转折期(如职业转换)的不确定性增加local_entropy_data = { 'cohort': ['1950s', '1960s', '1970s', '1980s', '1990s'], 'local_entropy': [0.38, 0.41, 0.45, 0.52, 0.56]}
def plot_local_entropy(data): plt.figure(figsize=(10, 6)) plt.bar(data['cohort'], data['local_entropy'], color='#8bd3c7') plt.title('Local Entropy Across Cohorts', fontsize=16) plt.xlabel('Birth Cohort', fontsize=14) plt.ylabel('Local Entropy', fontsize=14) plt.ylim(0, 1) plt.show()
# 主执行函数def main(): # 分别绘制三种熵的变化 plot_cross_sectional_entropy(cross_sectional_data) plot_longitudinal_entropy(longitudinal_data) plot_local_entropy(local_entropy_data)
# 运行主函数if __name__ == '__main__': main()
"""熵分析深度解读:
1. 横截面熵(Cross-Sectional Entropy) - 反映特定时间点的状态分布多样性 - 揭示社会在某一时刻的多元化程度 - 从0.40上升到0.60,显示职业选择越来越开放
2. 纵向熵(Longitudinal Entropy) - 展现个人整个生命历程的复杂性 - 追踪个人职业轨迹的不可预测性 - 从0.42上升到0.62,表明生命路径变得更加多样
3. 局部熵(Local Entropy) - 捕捉生命关键转折期的不确定性 - 聚焦特定时间窗口的状态变化 - 从0.38上升到0.56,说明关键时期变化越来越复杂
理论支持:- 支持"生命历程去标准化"理论- 反映社会结构的深层转型- 驱动因素包括教育、技术、经济和社会观念变革"""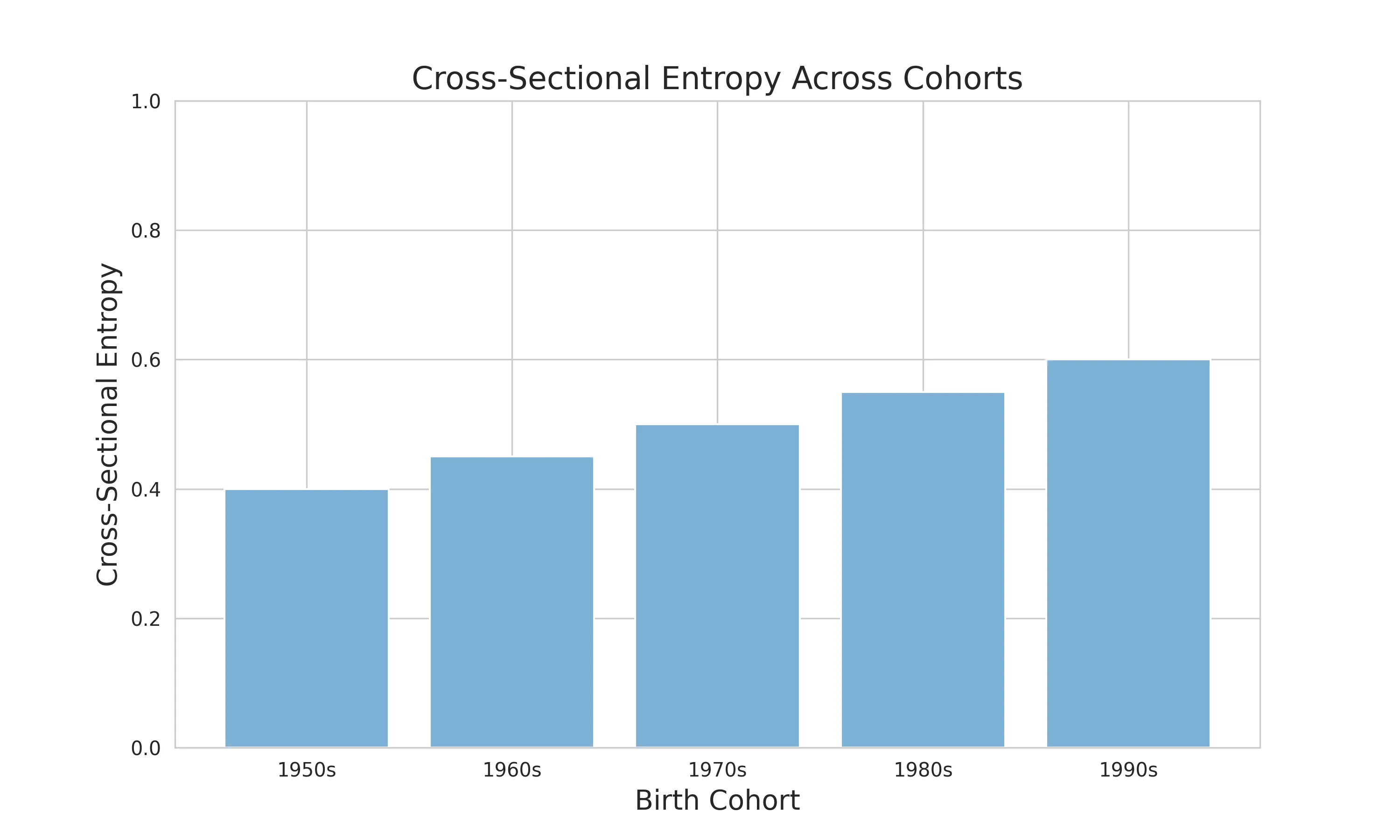
结果解读#
生命历程去标准化理论#
- 趋势证据
- 三种熵指标均呈现持续上升趋势
- 从1950年代到1990年代,生活轨迹变得更加多元和复杂
- 深层社会变迁
- 职业选择更加开放
- 个人发展路径更加非线性
- 社会流动性显著增加
- 驱动因素
- 教育普及
- 技术革新
- 经济结构转型
- 社会观念变革
小结#
- 多维度熵分析
- 横截面熵:揭示同期状态多样性
- 纵向熵:展现个人轨迹复杂性
- 局部熵:捕捉关键转折期
- 趋势一致性
- 三种熵指标同步上升
- 强有力地支持”去标准化”理论
- 社会变迁的量化描述
- 超越传统静态分析
- 动态捕捉社会结构变迁
未来研究方向
- 跨代际比较
- 不同社会群体的熵差异
- 熵指标与社会流动性的关联
生命轨迹的熵增长不仅是数值变化,更是社会深层结构转型的微观映射。熵,也能作为理解现代社会复杂性的桥梁。
总结:选择合适的熵指标#
针对不同研究问题,应选择不同类型的熵:
| 熵类型 | 标准化目的 | 主要优势 |
|---|---|---|
| 横截面熵 | 消除不同时间点状态分布的绝对差异 | 便于跨时间、跨群体比较 |
| 纵向熵 | 标准化个人轨迹的复杂性 | 减少序列长度和状态数量的影响 |
| 局部熵 | 归一化特定时间窗口的变化强度 | 提供可比较的转折期强度指标 |
在社会序列分析中,我们给通用熵”披上外衣”(标准化为横截面熵、纵向熵、局部熵)的根本原因是:标准化能够将复杂的社会动态转换为可比较、可解释的数值。原始熵容易受到序列长度、状态数量的影响,而标准化后的熵指标可以:
- 消除技术性差异
- 提供直观的0-1尺度
- 增强跨群体、跨时间的比较性
- 降低数据分析的随意性
简而言之,标准化是将社会复杂性转化为可理解语言的关键工具。
学习加餐:为什么 AI 领域也关心 Entropy?#
信息熵在机器学习和人工智能中扮演着很重要的角色,尤其是在建模时序数据、理解用户行为轨迹、增强模型解释性等方面。
信息熵(Entropy)是衡量“数据不确定性”最基本的工具。在机器学习中,它常被用来:
- 在决策树(如 ID3, C4.5)中选择划分特征;
- 衡量模型预测结果的“置信度”或“混乱程度”;
- 分析分类结果中样本分布是否平衡;
- 或者直接作为输入特征,表示一个用户或序列的“多样性”水平,用于后续聚类或监督学习。
推荐阅读:
Barbiero, P., Ciravegna, G., Giannini, F., Liò, P., Gori, M., & Melacci, S. (2022). Entropy-based logic explanations of neural networks *In Proceedings of the AAAI Conference on Artificial Intelligence, 36(6), 6046–6054.