Skip to content

信息熵在社会序列分析中的应用（三）：局部熵

· 14 min

在当代社会研究中，个体生命轨迹愈发呈现出多样化与非线性的特征：人们的教育路径不再单一，职业经历频繁变动，婚育模式也更加多元。

在这一背景下，如何量化这种轨迹的复杂性与多样性？

信息熵作为衡量“不确定性”的核心指标，提供了一种简洁而有力的解决方案。

本系列文章将围绕“信息熵在社会序列分析中的应用”展开，结合实际示例，从通用熵的基本概念，到横截面熵、纵向熵、局部熵，再到综合指标与实战案例，系统讲解如何用熵来刻画个体路径、群体差异和社会变迁。

局部熵（Local Entropy）可以帮助我们识别生命历程中的关键转折期。你可能会问，为什么这个函数跟上面的纵向熵是共用的同一个函数 seqient()？因为它们都衡量的是单个序列的复杂度，只是特点不同，函数使用的参数也不同。

局部熵是在序列分析中用于识别”不稳定性热点”的一种方法。它通过分析序列的局部窗口（比如3年）来揭示生命轨迹中变化最剧烈的时期。

局部熵与纵向熵的核心区别

  1. 局部熵其实可以称为浓缩成窗口阶段版的纵向熵，因为纵向熵是所有时间点都会计算这一个时间点内所有人的平均熵。
  2. 但局部熵则是不计算每个时间点，而是将比如这里6个时间点浓缩成三个时间窗口，计算每个时间窗口的所有人的平均熵

因此，相比于纵向熵是直接：

# 计算所有序列的纵向熵
long_entropies <- seqient(myseq)

局部熵，则是需要选择合适的窗口大小：

基本的局部熵计算：

# 使用seqient函数计算局部熵
# h参数定义滑动窗口的大小
local_entropy <- seqient(myseq, h=3)

更详细的局部熵分析：

# 更复杂的局部熵计算
local_entropy <- seqsloc(myseq,
                         method="entropy",  # 使用熵作为局部不确定性度量
                         window=3,          # 窗口大小为3
                         weighted=TRUE)     # 是否使用加权方法

当然，我们肯定还是要可视化局部熵：

# 绘制局部熵
plot(local_entropy,
     main="生命历程局部不确定性",
     xlab="时间/年龄",
     ylab="局部熵")

关键参数解释：

具体理解关键特征#

1. 窗口分析#

窗口（Window）是一种分析方法，通过在数据序列中移动固定大小的区间来捕捉局部特征。

典型应用场景

  1. 社会学研究
  1. 经济学
  1. 生命历程研究

窗口分析的具体示例

# 假设追踪一个人的职业生涯序列
career_sequence = [
    '学生', '学生', '实习',
    '兼职', '全职', '全职',
    '失业', '继续教育', '全职'
]


# 3年窗口分析
def analyze_window(sequence, window_size=3):
    windows = []
    for i in range(len(sequence) - window_size + 1):
        window = sequence[i:i+window_size]
        windows.append(window)
    return windows


# 计算每个窗口的熵
def calculate_window_entropy(windows):
    entropies = []
    for window in windows:
        # 计算窗口内状态分布的熵
        unique, counts = np.unique(window, return_counts=True)
        probabilities = counts / len(window)
        entropy = -np.sum(probabilities * np.log2(probabilities))
        entropies.append(entropy)
    return entropies

窗口分析的关键特征

  1. 灵活性
  1. 局部聚焦
  1. 动态捕捉

不同学科的窗口分析应用

  1. 心理学
  1. 流行病学
  1. 金融学

窗口大小的选择

实践建议

  1. 尝试不同窗口大小
  2. 结合理论背景
  3. 进行敏感性分析

窗口分析本质上是一种动态、灵活的方法，帮助我们从宏观序列中提取局部特征，揭示复杂系统的微观变化机制。

2. 变化检测#

实际意义举例#

假设我们在追踪一个人的职业生涯：

年龄   状态序列
20岁   学生 → 学生 → 学生
21岁   学生 → 实习 → 兼职
22岁   全职 → 全职 → 全职
23岁   全职 → 失业 → 继续教育
24岁   继续教育 → 全职 → 全职

局部熵分析可能显示：

import matplotlib.pyplot as plt


def generate_more_realistic_sequences(n_sequences=100, sequence_length=6):
    """
    生成更贴近生命历程的序列
    模拟典型的生命轨迹变化
    """
    sequences = []
    states = ['学生', '实习', '兼职', '全职', '失业', '继续教育']


    for _ in range(n_sequences):
        # 模拟典型生命轨迹
        seq = []
        # 早期：变化多
        seq.extend(['学生', '学生', '实习'])


        # 中期：逐渐稳定
        if np.random.random() < 0.7:
            seq.extend(['兼职', '全职', '全职'])
        else:
            seq.extend(['全职', '失业', '继续教育'])


        # 确保序列长度一致
        while len(seq) < sequence_length:
            seq.append(seq[-1])


        sequences.append(seq)


    return sequences


def calculate_local_entropy(sequences, window_size=3):
    """
    计算序列的局部熵
    """
    local_entropies = []
    for t in range(len(sequences[0]) - window_size + 1):
        local_windows = [seq[t:t+window_size] for seq in sequences]


        window_entropies = []
        for window in local_windows:
            unique, counts = np.unique(window, return_counts=True)
            probabilities = counts / len(window)


            window_entropy = -np.sum(probabilities * np.log2(probabilities))
            window_entropies.append(window_entropy)


        local_entropies.append(np.mean(window_entropies))


    return local_entropies


# 生成序列
sequences = generate_more_realistic_sequences(n_sequences=100, sequence_length=6)


# 计算局部熵
local_entropies = calculate_local_entropy(sequences)


# 可视化
plt.figure(figsize=(10, 6))
plt.plot(local_entropies, marker='o')
plt.title('Local Entropy of Life Course Sequences')
plt.xlabel('Time Window')
plt.ylabel('Local Entropy')
plt.grid(True)


# 修改 x 轴刻度为整数
plt.xticks(range(len(local_entropies)), range(len(local_entropies)))


plt.savefig('local_entropy.png', dpi=300)
plt.show()

这段代码实现了局部熵的计算和可视化，具体解释如下：

假设追踪100名毕业生的职业状态：

假设其中的一个人的职业生涯序列是：

[学生, 学生, 实习, 兼职, 全职, 全职, 失业, 继续教育, 全职]

对于窗口大小为3的情况：

  1. 第一个窗口 [学生, 学生, 实习]
  1. 第二个窗口 [学生, 实习, 兼职]
  1. 第三个窗口 [实习, 兼职, 全职]

下面图像展示了这位同学的的局部熵演变情况（不是所有人）

熵值
 ↑
 |      *
 |    *     *
 |  *           *
 +-------------------→ 时间窗口
   1   2   3   4   5

而总体生成的100个毕业生的局部熵图像，则长下面这样：

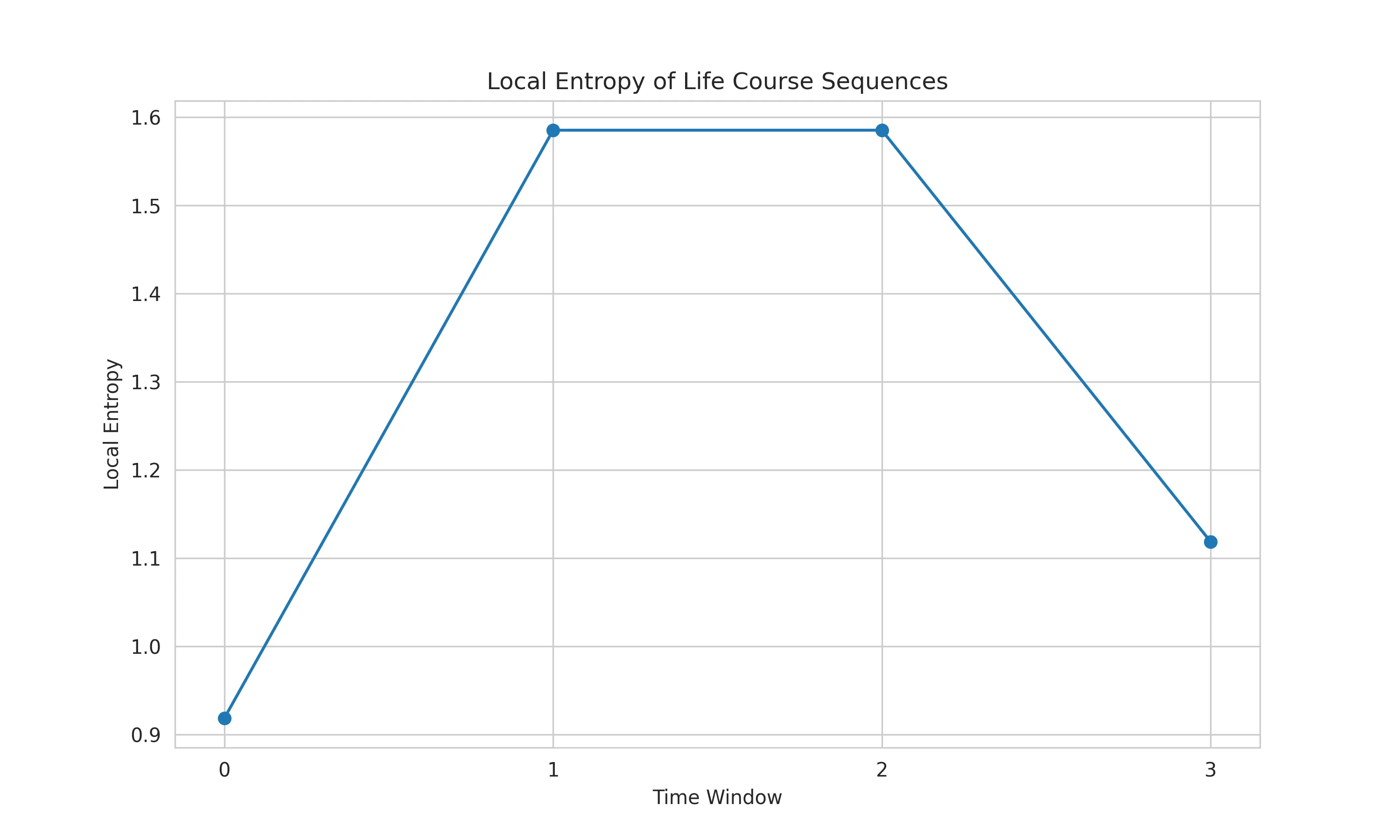
local_entropy

代码详细解析：

  1. 输入参数
  1. 计算过程 
    for t in range(len(sequences[0]) - window_size + 1):
  1. 局部窗口提取 
    local_windows = [seq[t:t+window_size] for seq in sequences]
  1. 熵值计算 
    # 计算窗口内状态分布
    unique, counts = np.unique(window, return_counts=True)
    probabilities = counts / len(window)
    

    # 计算熵
    window_entropy = -np.sum(probabilities * np.log2(probabilities))
  1. 平均局部熵 
    local_entropies.append(np.mean(window_entropies))
局部熵与纵向熵的核心区别

  1. 局部熵其实可以称为浓缩成窗口阶段版的纵向熵，因为纵向熵是所有时间点都会计算这一个时间点内所有人的平均熵。
  2. 但局部熵则是不计算每个时间点，而是将比如这里6个时间点浓缩成三个时间窗口，计算每个时间窗口的所有人的平均熵
  1. 可视化
plt.plot(local_entropies, marker='o')

局部熵 vs 纵向熵#

注意

通过局部熵，我们可以更精细地理解生命历程中的动态变化过程，发现那些看似平静但实际充满可能性的关键时期。

总结#

局部熵的实际应用场景

  1. 职业生涯研究
  1. 生命历程分析

关键点

总之，时间窗口分析帮助我们：