在当代社会研究中,个体生命轨迹愈发呈现出多样化与非线性的特征:人们的教育路径不再单一,职业经历频繁变动,婚育模式也更加多元。
在这一背景下,如何量化这种轨迹的复杂性与多样性?
信息熵作为衡量“不确定性”的核心指标,提供了一种简洁而有力的解决方案。
本系列文章将围绕“信息熵在社会序列分析中的应用”展开,结合实际示例,从通用熵的基本概念,到横截面熵、纵向熵、局部熵,再到综合指标与实战案例,系统讲解如何用熵来刻画个体路径、群体差异和社会变迁。
想象你追踪一个人的职业生涯。纵向熵就像是衡量这个人职业道路”变幻莫测程度”的尺度。
- 低熵:就像一条笔直的职业道路
- 例子:小明从大学毕业后一直在同一家公司做同一份工作
- 状态变化很少,生活轨迹非常稳定
- 高熵:就像一条曲折多变的职业道路
- 例子:小红从兼职到全职,再到创业,中间还去进修,职业状态变化频繁
- 状态变化很多,生活轨迹充满不确定性
纵向熵与横截面熵不同,它关注的是单个序列内部的状态变化,用于衡量”一条序列中状态分布的多样性(所以叫做序列内熵,因为我们只看这条序列,不看别的序列)“。如果说横截面熵是测量某一时间点所有样本的多样性,那么纵向熵则是测量单个样本整个生命历程的多样性。
大家要记住一句话:Longitudinal Entropy (纵向熵) = Within Sequence Entropy (序列内熵)。并且在 R 包 TraMineR 中,用的是 seqient() 函数。
计算方法#
纵向熵基于单个序列中,各状态的比例分布来计算,比如:
- 序列”FFFPPPUUU”的纵向熵较高
- “FFFFFFFFF”的纵向熵为0
再来举个例子:
- 如果一个人的生命历程中95%的时间都在同一状态(例如全职工作),纵向熵将非常低
- 如果一个人平均分配时间在学习、工作、家庭等多种状态,纵向熵将较高
总体来说
- 个体序列的复杂度:纵向熵衡量单个序列中状态出现的均匀程度
- 高纵向熵:表示个体在生命历程中经历了多种状态,且各状态出现时间较为均衡
- 低纵向熵:表示个体生命历程被某一种或少数几种状态主导
具体在 TraMineR 中是如何调用这个函数的呢?#
# 计算每个序列的纵向熵longitudinal_entropies <- seqient(myseq)
# 标准化的纵向熵longitudinal_entropies_norm <- seqient(myseq, norm=TRUE)TraMineR 中的源代码点击这里查看。
这个seqient()函数计算的是序列的”状态不确定性”(Within Sequence Entropy)。具体来说:
- 输入:
- 一组序列数据(每个序列表示一个个体的状态变化)
- 序列中的每个元素代表不同的状态
- 主要计算过程:
- 对每个个体的序列计算熵值
- 熵值反映了该序列状态变化的复杂性和不确定性
- 输出结果:
- 一个矩阵,每一行对应一个个体
- 列名为”Entropy”
- 每个值代表该个体序列的熵值
- 关键参数:
norm=TRUE:将熵值标准化到0-1范围- 0:表示序列状态完全确定(只有一种状态)
- 1:表示序列状态最大程度变化
举个具体例子,假设有三个人的职业状态序列:
- 小明:F → F → F → F(全职)
- 小红:F → P → U → E(变化多端)
- 小李:F → F → P → P(部分变化)
计算结果可能是:
- 小明:熵值接近0
- 小红:熵值接近1
- 小李:熵值中等
常见的分析是,我们会用这个指标来比较不同群体生活轨迹的变化程度,比如下面的例子中,我们会求得每个组个体的纵向熵的平均数。
可视化与分析#
# 计算所有序列的纵向熵long_entropies <- seqient(myseq)
# 绘制纵向熵的分布hist(long_entropies, main="序列纵向熵分布", xlab="纵向熵值", col="lightblue")
# 按分组比较纵向熵boxplot(long_entropies ~ group_variable, data=your_data_frame, main="不同群体的生命历程复杂度比较", xlab="群体类别", ylab="纵向熵")我们如果用 Python 来计算,代码则为:
import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfrom scipy.stats import entropy
# 模拟生命历程序列数据# 假设我们有100个个体的就业状态序列# 状态: F (全职), P (兼职), U (失业), E (继续教育)np.random.seed(42)
# 生成示例序列数据def generate_sequences(n_sequences=100, sequence_length=3): # 状态定义 states = ['F', 'P', 'U', 'E']
# 序列生成规则(这里是一个简化的模拟) sequences = [] for _ in range(n_sequences): seq = [] # 第一个时间点状态分布接近原始数据 first_dist = [0.4, 0.1, 0.35, 0.15] first_state = np.random.choice(states, p=first_dist) seq.append(first_state)
# 后续时间点状态转移 for t in range(1, sequence_length): if seq[-1] == 'F': # 全职工作倾向于保持 next_state = np.random.choice(states, p=[0.8, 0.1, 0.05, 0.05]) elif seq[-1] == 'P': # 兼职倾向于转全职或失业 next_state = np.random.choice(states, p=[0.5, 0.2, 0.2, 0.1]) elif seq[-1] == 'U': # 失业倾向于找工作或继续教育 next_state = np.random.choice(states, p=[0.4, 0.1, 0.3, 0.2]) else: # 继续教育倾向于全职或继续学习 next_state = np.random.choice(states, p=[0.4, 0.1, 0.1, 0.4]) seq.append(next_state)
sequences.append(seq)
return sequences
# 计算序列的纵向熵def calculate_longitudinal_entropy(sequences): # 计算每个序列的状态分布 entropies = [] for seq in sequences: # 计算序列中每个状态的分布 unique, counts = np.unique(seq, return_counts=True) probabilities = counts / len(seq)
# 计算序列的熵 seq_entropy = entropy(probabilities, base=2) entropies.append(seq_entropy)
return entropies
# 分组纵向熵计算(模拟)def calculate_group_entropies(sequences): # 假设我们根据某些特征将序列分为两组 # 这里简单地将序列随机分为两组 np.random.seed(42) group_labels = np.random.choice(['Group A', 'Group B'], size=len(sequences))
# 计算每个组的纵向熵 group_entropies = {} for group in ['Group A', 'Group B']: group_sequences = [seq for seq, label in zip(sequences, group_labels) if label == group] group_entropies[group] = calculate_longitudinal_entropy(group_sequences)
return group_entropies, group_labels
# 主分析和可视化def main(): # 生成序列数据 sequences = generate_sequences()
# 计算纵向熵 longitudinal_entropies = calculate_longitudinal_entropy(sequences)
# 计算分组熵 group_entropies, group_labels = calculate_group_entropies(sequences)
# 设置清新的配色方案 fresh_colors = ['#7eb0d5', '#8bd3c7', '#ffb55a', '#fd7f6f', '#bd7ebe'] plt.style.use('seaborn-v0_8-whitegrid')
# 创建画布 fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10), gridspec_kw={'height_ratios': [1, 1.2]})
# 直方图:纵向熵分布 ax1.hist(longitudinal_entropies, bins=20, color=fresh_colors[0], edgecolor='black', alpha=0.7) ax1.set_title('Longitudinal Entropy Distribution of Employment Sequences', fontsize=16, pad=20) ax1.set_xlabel('Longitudinal Entropy', fontsize=14) ax1.set_ylabel('Frequency', fontsize=14) ax1.spines['top'].set_visible(False) ax1.spines['right'].set_visible(False)
# 添加平均熵值标注 mean_entropy = np.mean(longitudinal_entropies) ax1.axvline(mean_entropy, color='red', linestyle='--', linewidth=2) ax1.text(mean_entropy*1.1, ax1.get_ylim()[1]*0.9, f'Mean Entropy: {mean_entropy:.3f}', color='red', fontsize=12, fontweight='bold')
# 箱线图:分组纵向熵比较 box_data = [group_entropies['Group A'], group_entropies['Group B']] bp = ax2.boxplot(box_data, patch_artist=True, boxprops=dict(facecolor=fresh_colors[2], alpha=0.7), medianprops=dict(color='red')) ax2.set_title('Longitudinal Entropy Comparison between Groups', fontsize=16, pad=20) ax2.set_xlabel('Group', fontsize=14) ax2.set_ylabel('Longitudinal Entropy', fontsize=14) ax2.set_xticklabels(['Group A', 'Group B']) ax2.spines['top'].set_visible(False) ax2.spines['right'].set_visible(False)
# 添加统计显著性检验(这里使用t检验作为示例) from scipy import stats t_stat, p_value = stats.ttest_ind(group_entropies['Group A'], group_entropies['Group B']) plt.figtext(0.5, 0.01, f't-test: t-statistic = {t_stat:.3f}, p-value = {p_value:.4f}', ha='center', fontsize=10, style='italic', color='gray')
plt.tight_layout() plt.subplots_adjust(bottom=0.1)
# 保存图形 plt.savefig('longitudinal_entropy_analysis.png', dpi=300) plt.show()
# 返回一些基本统计信息 return { 'mean_entropy': mean_entropy, 'group_a_mean_entropy': np.mean(group_entropies['Group A']), 'group_b_mean_entropy': np.mean(group_entropies['Group B']), 't_statistic': t_stat, 'p_value': p_value }
# 运行主分析if __name__ == '__main__': results = main() print("Longitudinal Entropy Analysis Results:") for key, value in results.items(): print(f"{key}: {value}")输出一:
Longitudinal Entropy Analysis Results:mean_entropy: 0.6835589588020848group_a_mean_entropy: 0.644976136822554group_b_mean_entropy: 0.7138740332145732t_statistic: -0.6216085479917747p_value: 0.5356426595744366输出二:
上面的这个Python脚本模拟了纵向熵(Longitudinal Entropy)的计算和可视化,借鉴了 R 中seqient函数的思路。主要步骤包括:
- 生成模拟的就业状态序列数据
- 计算每个序列的纵向熵
- 绘制纵向熵的分布直方图(第一个子图)
- 模拟分组(A组和B组)并进行箱线图比较(第二个子图)
- 使用t检验比较两组之间的熵差异
具体函数而言:
generate_sequences(): 生成带有状态转移规则的序列calculate_longitudinal_entropy(): 计算序列的熵calculate_group_entropies(): 将序列分组并计算组内熵main(): 执行数据分析和可视化
让我们详细解读这个纵向熵分析的结果:
主要统计结果(也就是打印出来的那些内容):
- 平均熵值(Mean Entropy):0.684
- 平均熵接近0.7,表明模拟的职业生涯不是完全固定(不接近0),也不是完全随机(不接近1),在 0.5-1之间,说明这组模拟数据的职业生涯变化程度中等偏高
- 分组平均熵值:
- A组:0.645
- B组:0.714
- B组的职业生涯轨迹略微更加复杂、变化更多
- 统计检验结果:
- t统计量:-0.622
- p值:0.536 远大于0.05
- 说明A组和B组的熵值差异不具有统计学显著性;换言之,两组的职业轨迹复杂性基本可以视为没有显著差异
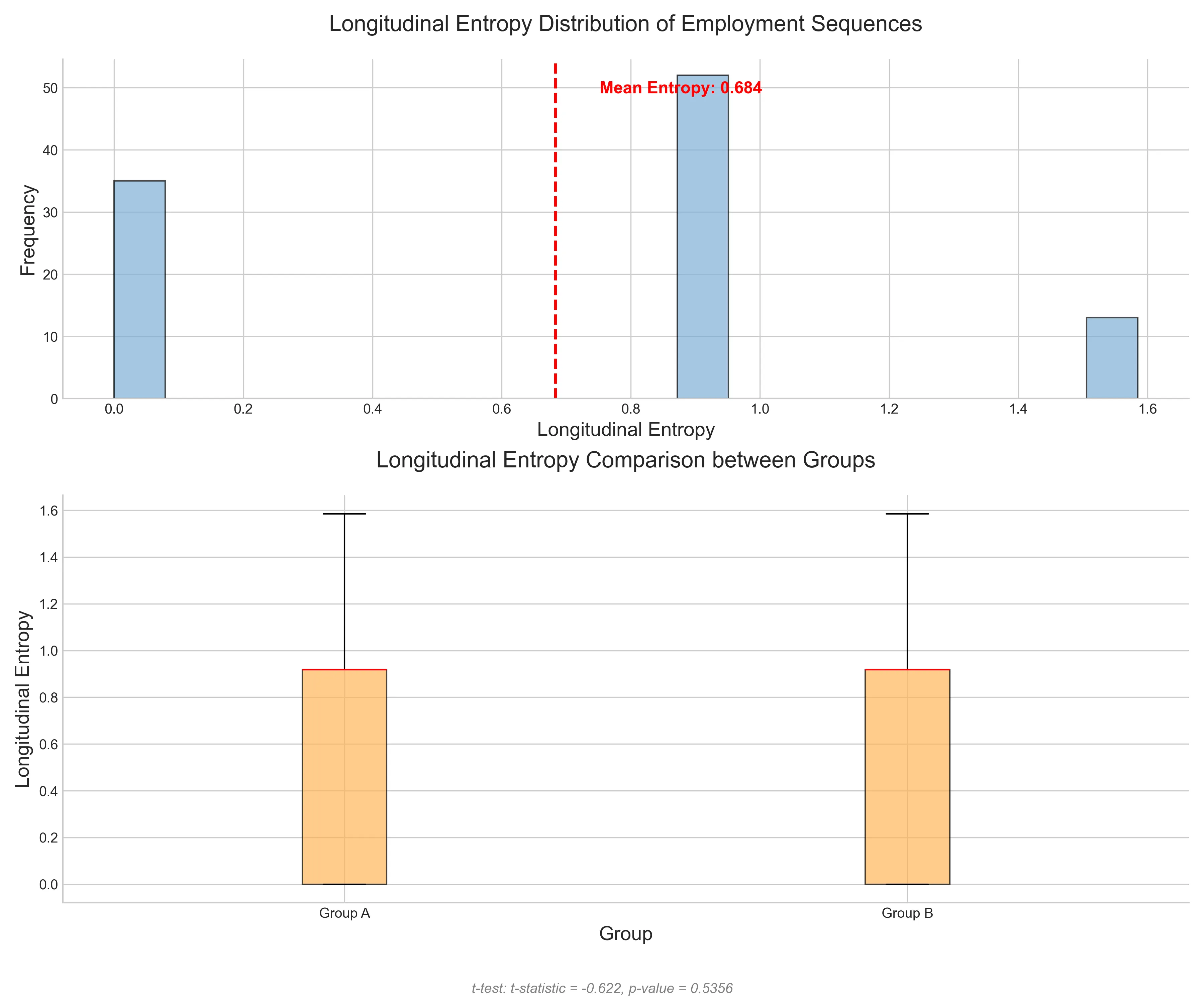
第一张图(直方图):
- X轴:纵向熵值
- Y轴:落入每个熵值区间的序列数量
- 红色虚线:平均熵值(0.684)
- 呈现略微右偏的分布,说明大部分序列的熵值集中在较低区间,但有少数序列熵值很高
第二张图(箱线图):
- 比较A组和B组的熵值分布
- B组的箱体略高,中位数(红线)更靠上
- 说明B组的职业轨迹变化程度略高于A组
如果要通俗比喻的话,我们可以想象两个毕业生群体:
- A组:职业道路比较稳定,变化不大
- B组:职业道路略微曲折,变化稍多
但这种差异并不显著,就像两个人的人生轨迹略有不同,但总体看起来很相似。 这个分析展示了一种通过熵值量化个人职业生涯复杂性的方法,帮助我们理解群体间职业轨迹的微妙差异。
纵向熵的高级应用#
- 与社会因素的关联分析:探索社会经济地位、性别、教育等因素如何影响生命历程的复杂度
# 线性回归分析影响因素lm_result <- lm(long_entropies ~ gender + education + social_class, data=your_data_frame)summary(lm_result)- 序列聚类与纵向熵:将序列按复杂度分组,探索不同复杂度的典型模式
# 根据纵向熵将序列分组entropy_groups <- cut(long_entropies, breaks=3, labels=c("低复杂度","中复杂度","高复杂度"))
# 绘制各组的代表序列seqdplot(myseq, group=entropy_groups, main="不同复杂度组的状态分布")- 纵向熵与状态转换:纵向熵与转换率的关系研究
# 计算序列转换率transition_rates <- seqtrate(myseq)
# 分析转换率与纵向熵的相关性plot(rowSums(transition_rates) ~ long_entropies, xlab="纵向熵", ylab="状态转换总率", main="复杂度与状态变化频率的关系")纵向熵与横截面熵的比较#
| 纵向熵 | 横截面熵 |
|---|---|
| 基于单个序列的状态分布 | 基于特定时间点所有序列的状态分布 |
| 衡量个体生命历程的复杂度 | 衡量集体在特定时间点的多样性 |
| 用于识别不同的个体生命轨迹类型 | 用于识别生命历程中的关键转折期 |
| 不随时间变化(每个序列一个值) | 随时间变化(每个时间点一个值) |
理论意义 - 纵向熵提供了一种量化生命历程稳定性与变动性的方法,有助于理解:
- 现代社会中生命历程的去标准化趋势
- 不同社会群体间生命机会的差异
- 社会政策对生命历程多样性的影响
通过纵向熵分析,我们可以更好地理解社会变迁如何影响个体生命历程的复杂性和多样性。