信息熵在社会序列分析中的应用（一）：通用熵和横截面熵

在当代社会研究中，个体生命轨迹愈发呈现出多样化与非线性的特征：人们的教育路径不再单一，职业经历频繁变动，婚育模式也更加多元。
在这一背景下，如何量化这种轨迹的复杂性与多样性？
信息熵作为衡量“不确定性”的核心指标，提供了一种简洁而有力的解决方案。
本系列文章将围绕“信息熵在社会序列分析中的应用”展开，结合实际示例，从通用熵的基本概念，到横截面熵、纵向熵、局部熵，再到综合指标与实战案例，系统讲解如何用熵来刻画个体路径、群体差异和社会变迁。

想象一下，我们有一群人的生活轨迹数据。小明从学校毕业后一直在同一家公司工作到退休；而小红则经历了多次求学、就业、育儿假和职业转换。如何量化这种差异？这就是社会序列的复杂度指标，尤其是信息熵的价值所在。

信息熵本质上是测量不确定性的工具。在社会序列中：

低熵值：生活状态单一、可预测（如小明的案例）
高熵值：状态多样、变化频繁（如小红的案例）

为什么研究者喜欢用熵？因为它能：

将复杂的生命轨迹简化为可比较的数字
客观比较不同群体的生活复杂度
追踪社会变迁（如现代社会生活轨迹更多元？）
评估政策影响（如育儿政策如何影响职业轨迹稳定性）

在这个教程中，我们会主要讲解序列分析的复杂度是什么、熵的概念，以及横截面熵。

复杂度计算：概述#

我们需要区分两种”复杂度（complexity）“概念：

算法复杂度：计算机科学中的时间复杂度(O(n log n))、空间复杂度(O(n))
序列复杂度：序列本身的多样性与变化程度

在序列分析中，复杂度指的是序列本身的多样性与变化程度，即一个序列使用了多少种不同的状态、这些状态切换的频率、状态分布是否均匀、出现顺序是否规律等。

信息熵(Entropy)：理论基础#

信息熵的概念#

信息熵是由信息论创始人Claude E. Shannon于1948年在经典论文”A Mathematical Theory of Communication”中提出的概念，用来量化信息的不确定性。

简单来说，信息熵衡量的是状态分布的平均程度或系统的不确定性。在序列分析中，它反映了一个人生活中经历的状态有多平均、是否偏向某些特定状态。

信息熵的数学公式#

香农熵的计算公式为：

\text{Entropy} = - \sum_{i=1}^{n} p_i \log_2 p_i

其中：

p_i 是状态 i 在序列中出现的频率(比例)
对所有出现过的状态求和

信息熵的物理学背景#

信息熵的形式与物理学中热力学熵的定义形式相似。Ludwig Boltzmann给出的熵公式为：

S = k \cdot \ln W

其中：

S：系统的熵
k：Boltzmann常数
W：系统可能的微观状态数

香农在命名时咨询了数学家John von Neumann(冯·诺依曼)，他建议使用”entropy”这个术语，因为”这个公式已经在热力学中使用”，而且”没人真正了解熵是什么，所以在任何讨论中你都会有优势”。

信息熵的单位：bit#

信息熵的单位是”bit”(信息位)，表示表达一个事件所需的平均二进制决策数量。例如：

公平硬币的熵值为1 bit，表示需要1个二进制位来编码结果
4面骰子(每面概率均等)的熵值为2 bits，表示需要2个二进制位来编码结果

信息熵的应用示例#

示例1：扔硬币和投骰子#

扔硬币(两种等可能结果)：

熵 = -(0.5 * log₂(0.5) + 0.5 * log₂(0.5)) = 1 bit

扔4面骰子(四种等可能结果)：

熵 = -4 * (0.25 * log₂(0.25)) = 2 bits

示例2：社会序列分析#

对于序列 [Student, Student, Student, Work, Work, Retired]：

状态	次数	比例 `p`
Student	3	0.5
Work	2	0.333
Retired	1	0.167

计算熵值：

Entropy = -[0.5*log₂(0.5) + 0.333*log₂(0.333) + 0.167*log₂(0.167)]
        ≈ -[-0.5 + -0.528 + -0.431]
        ≈ 1.459 bits

这表示序列有中等偏高的不均衡性和多样性。

极端情况对比#

全部相同状态的序列(如 [Work, Work, Work, Work, Work])：熵 = 0 (最低复杂度)
均匀分布不同状态的序列(如 [A, B, C, D, E])：熵 = 最大值 (最高复杂度)

熵与其他复杂度指标(如波动度Turbulence)的区别在于，熵只关注状态使用和分布，而波动度还考虑状态切换频率和出现顺序等因素。

各种熵在社会序列分析中的应用#

1. 通用熵 Entropy#

TraMineR 在 entropy() 中实现了Shannon熵（信息熵）的标准实现，它是信息论中的基础概念。具体的代码链接，点击这里。

## Compute the entropy of a distribution

entropy <- function(distrib, base=exp(1))
  {
    distrib <- distrib[distrib!=0]
    p <- distrib/sum(distrib)
    e <- -sum(p*log(p, base=base))
    return(e)
  }

在序列分析中，这个函数可以用于计算不同类型的熵，包括横截面熵、纵向熵、局部熵，具体取决于传入的分布数据。函数主要做的步骤如下：

函数接收一个概率分布（或可以转换为概率分布的计数/频率）作为输入
移除零概率事件（distrib[distrib!=0]）
将输入标准化为概率分布（p <- distrib/sum(distrib)）
应用Shannon熵公式计算：-sum(p*log(p))
允许使用不同的对数底（默认为自然对数，base=exp(1)）

在序列分析中，这个函数被用在不同场景：

横截面熵计算时，distrib是某一时间点上所有序列的状态分布
纵向熵计算时，distrib是单个序列中各状态的出现频率分布
局部熵计算时，distrib是滑动窗口内的状态分布

例如，在下面我们就会看到：

cross_entropies <- apply(cross_section_dist$Frequencies, 1, entropy)

这里通过apply函数对每个时间点的状态分布计算熵，得到的就是横截面熵。

而在计算纵向熵时，可能会用到类似的代码：

# 假设seqtab是序列状态频率表
long_entropies <- apply(seqtab, 1, entropy)

所以这个函数本身是熵的一般计算工具，而它计算的是哪种具体类型的熵，取决于用户想要传入的是什么样的分布数据。

2. 横截面熵（cross-sectional entropy）：`seqstatd`#

想了解特定时间点（如25岁时）全体样本的状态多样性？这就需要横截面熵。横截面熵是按照时间点分别计算的熵，用于衡量”在特定时间点上所有序列的状态分布有多分散”。

因此，横截面熵与通用熵的区别在于输入分布的不同：

通用熵：接受任何概率分布作为输入
横截面熵：特别关注”时间 $t$ 时所有序列的状态分布”作为输入分布，因此，输入的分布只有每个时间点（比如这一年）的所有序列的状态分布

# 计算每个时间点的状态分布
cross_section_dist <- seqstatd(myseq, time.varying=TRUE)

# 计算每个时间点的熵
cross_entropies <- apply(cross_section_dist$Frequencies, 1, entropy)

你可能要问，什么叫做输入这个函数所需要的分布（distribution）？在熵的计算中，“输入分布”就是我们要计算熵值的那组数据或概率。对于横截面熵，这个输入分布具体指的是：在某个特定时间点，所有人处于各种不同状态的比例。

具体例子

假设我们跟踪了100名大学毕业生的就业状态，状态包括：

F: 全职工作
P: 兼职工作
U: 失业
E: 继续教育

在毕业后不同时间点，我们观察到的状态分布是：

毕业后3个月：

40人全职工作 (F: 40%)
10人兼职工作 (P: 10%)
35人失业 (U: 35%)
15人继续教育 (E: 15%)

毕业后1年：

60人全职工作 (F: 60%)
15人兼职工作 (P: 15%)
15人失业 (U: 15%)
10人继续教育 (E: 10%)

毕业后3年：

85人全职工作 (F: 85%)
5人兼职工作 (P: 5%)
5人失业 (U: 5%)
5人继续教育 (E: 5%)

现在，对每个时间点，我们将这些百分比作为”输入分布”计算熵，那么也就算出来了这个数据集整体来说，横截面的熵到底是多少：

# 定义分布
dist_3months <- c(0.40, 0.10, 0.35, 0.15)  # 毕业后3个月的状态分布
dist_1year <- c(0.60, 0.15, 0.15, 0.10)    # 毕业后1年的状态分布
dist_3years <- c(0.85, 0.05, 0.05, 0.05)   # 毕业后3年的状态分布

# 使用entropy函数计算各时间点的横截面熵
entropy_3months <- entropy(dist_3months)
entropy_1year <- entropy(dist_1year)
entropy_3years <- entropy(dist_3years)

如果用 Python 计算和画图，代码如下：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.gridspec import GridSpec

# 设置比较清新的配色方案
fresh_colors = ['#7eb0d5', '#8bd3c7', '#ffb55a', '#fd7f6f', '#bd7ebe']
plt.style.use('seaborn-v0_8-whitegrid')

# 定义分布
dist_3months = np.array([0.40, 0.10, 0.35, 0.15])  # 毕业后3个月的状态分布
dist_1year = np.array([0.60, 0.15, 0.15, 0.10])    # 毕业后1年的状态分布
dist_3years = np.array([0.85, 0.05, 0.05, 0.05])   # 毕业后3年的状态分布

# 计算熵值
def entropy(dist):
    return -np.sum(dist * np.log(dist))

entropy_3months = entropy(dist_3months)
entropy_1year = entropy(dist_1year)
entropy_3years = entropy(dist_3years)

# 英文时间点
time_points = ["3 Months", "1 Year", "3 Years"]
entropy_values = [entropy_3months, entropy_1year, entropy_3years]

# 创建画布
fig = plt.figure(figsize=(12, 10))
gs = GridSpec(2, 1, height_ratios=[1, 1.2])

# 绘制熵值变化图
ax1 = fig.add_subplot(gs[0])
ax1.plot(time_points, entropy_values, marker='o', linestyle='-', color=fresh_colors[0],
         linewidth=3, markersize=10)
ax1.set_ylim([0, max(entropy_values) * 1.2])

# 添加数据标签
for i, val in enumerate(entropy_values):
    ax1.text(i, val + 0.05, f'{val:.3f}', ha='center', va='bottom',
             fontsize=13, color=fresh_colors[0], fontweight='bold')

ax1.set_title('Cross-sectional Entropy of Graduate Employment Status', fontsize=16, pad=20)
ax1.set_ylabel('Entropy', fontsize=14)
ax1.grid(True, alpha=0.3)
ax1.spines['top'].set_visible(False)
ax1.spines['right'].set_visible(False)

ax1.annotate('Entropy decreases over time, indicating convergence to uniformity',
             xy=(1, entropy_3years), xytext=(1.2, entropy_1year),
             fontsize=12, color='gray',
             arrowprops=dict(arrowstyle='->', color='gray', alpha=0.7))

# -------------------------


# 绘制堆叠柱状图
ax2 = fig.add_subplot(gs[1])
status_names = ['Full-time (F)', 'Part-time (P)', 'Unemployed (U)', 'Education (E)']

bar_width = 0.6
bottoms = np.zeros(3)
for i, status in enumerate(status_names):
    values = [dist_3months[i], dist_1year[i], dist_3years[i]]
    bars = ax2.bar(time_points, values, bar_width, bottom=bottoms,
                  label=status, color=fresh_colors[i % len(fresh_colors)])

    # 添加百分比标签
    for j, bar in enumerate(bars):
        height = bar.get_height()
        if height > 0.05:  # 只为较大的比例添加标签
            ax2.text(bar.get_x() + bar.get_width()/2, bottoms[j] + height/2,
                    f'{values[j]:.0%}', ha='center', va='center',
                    color='white', fontsize=12, fontweight='bold')

    bottoms += values

ax2.set_title('Distribution of Graduate Employment Status Over Time', fontsize=16, pad=20)
ax2.set_ylabel('Proportion', fontsize=14)
ax2.set_ylim([0, 1.05])
ax2.set_yticks(np.arange(0, 1.1, 0.2))
ax2.set_yticklabels([f'{int(x*100)}%' for x in np.arange(0, 1.1, 0.2)])
ax2.spines['top'].set_visible(False)
ax2.spines['right'].set_visible(False)
ax2.legend(title='Employment Status', bbox_to_anchor=(1.05, 1), loc='upper left', fontsize=12)

plt.figtext(0.5, 0.01, 'Over time, graduates converge from diverse states to primarily full-time work, reflected by decreasing entropy',
           ha='center', fontsize=12, style='italic', color='gray')

plt.tight_layout()
plt.subplots_adjust(bottom=0.1)

plt.savefig('cross_sectional_entropy', dpi=300)

plt.show()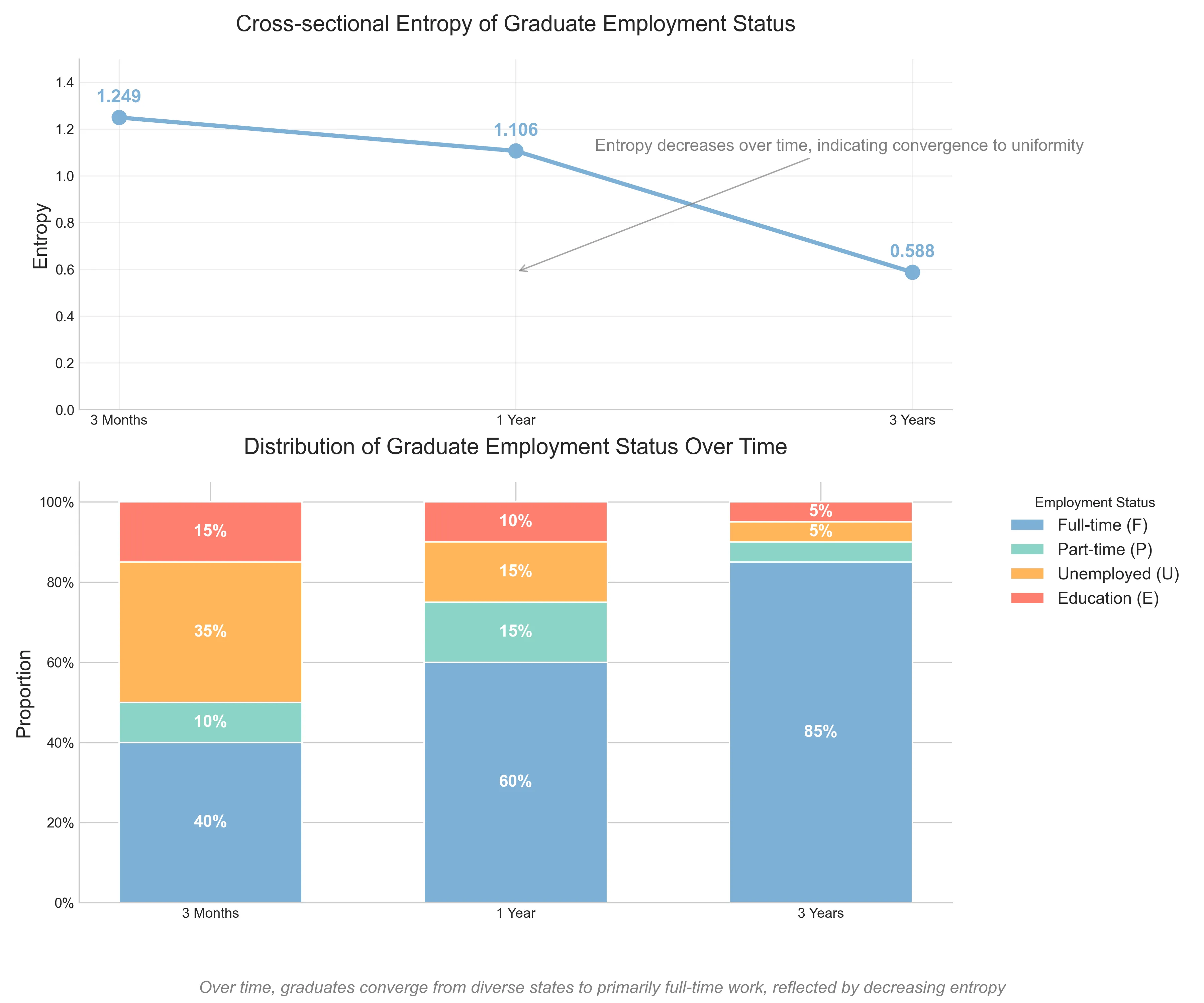

cross-sectional-entropy

我们有三个时间点，还记得我们说这类熵主要做的是横截面吧？横截面就是我们不管其他时间点，就只看当下的这个时间。那么在数据里，有三个时间点，每个时间点的结果解释如下：

毕业后3个月：状态分布较为分散（下面的条形图📊能看出来），横截面熵较高（从上面的折线图里的那个点能看出来）
毕业后1年：状态开始集中于全职工作，熵值降低
毕业后3年：绝大多数人都是全职工作，熵值更低

`seqstatd()`函数解释#

在R代码中，我们使用seqstatd()函数来计算每个时间点的状态分布，并返回一个stslist.statd类型的列表，包含三个主要组件：

Frequencies: 一个矩阵，显示每个时间点各状态的比例分布

行：可能的状态（如F, P, U, E）
列：时间点（如月份1, 月份2, 月份3…）
值：每个时间点处于各状态的序列比例（0-1之间）

ValidStates: 一个向量，表示每个时间点有效（非缺失）的状态数量
Entropy: 一个向量，包含每个时间点的熵值

如果norm=TRUE（默认），熵值被标准化到0-1之间
熵值代表相应时间点上状态分布的多样性/不确定性

对于我们之前讨论的毕业生就业状态例子（3个时间点、4种状态），seqstatd()函数的输出会是这样：

# 基于Python计算的数据
# 时间点: 毕业后3个月, 1年, 3年
# 状态: F(全职), P(兼职), U(失业), E(教育)

$Frequencies
          3 Months   1 Year   3 Years
F           0.40      0.60      0.85
P           0.10      0.15      0.05
U           0.35      0.15      0.05
E           0.15      0.10      0.05

$ValidStates
3 Months  1 Year  3 Years
   100     100      100

$Entropy
 3 Months   1 Year  3 Years
  1.129     1.019    0.613

这个输出清晰地展示了：

状态分布变化：从Frequencies中可以看到，全职工作(F)的比例从40%增加到了85%，而其他三种状态的比例都有所下降。
状态多样性变化：从Entropy中可以看到，熵值从1.129降至0.613，表明状态分布从较为多样化变为高度集中。这与Python代码中计算的结果一致，其中：

entropy_3months = -np.sum(dist_3months * np.log(dist_3months)) ≈ 1.129
entropy_1year = -np.sum(dist_1year * np.log(dist_1year)) ≈ 1.019
entropy_3years = -np.sum(dist_3years * np.log(dist_3years)) ≈ 0.613

有效样本量：ValidStates显示每个时间点都有100个有效观测（假设样本量为100）。

可视化很重要#

当然，一图胜千言。因此，我们更多用可视化的方式来展示横截面熵，因此，在 R 中，跑完 seqstatd() 之后，我们都会通过plot(seqstatd(...), type = "Ht")绘制随时间变化的熵曲线，比如：

# 绘制横截面熵随时间变化的曲线
plot(cross_entropies, type="l",
     xlab="年龄", ylab="横截面熵",
     main="生命历程的集体节奏")

当我们调用plot(seqstatd(...), type="Ht")时，会生成熵值随时间变化的线图（刚刚我们已经看过图了）。
当我们调用plot(seqstatd(...), type="d")时，会生成频率分布的堆叠面积图（刚刚的下方图）。

我们再总结一下，如何理解图：

熵值低的时期：大多数序列处于相同状态
熵值高的时期：序列状态多样化
熵值下降的时期：序列状态再次趋于一致

这些图形直观地展示了我们之前讨论的状态分布变化和熵值下降，帮助我们理解毕业生就业状态如何从多样化转向以全职工作为主导的过程。

以上的毕业生例子中，横截面熵的变化趋势（从高到低）表明：随着时间推移，毕业生的就业状态从多样化逐渐变得同质化，大部分人都进入了全职工作状态；而这种变化，正是横截面熵能够捕捉的集体生命历程节奏。

代码中为什么会有两个熵的指标？#

如果具体看代码，还能发现，seqstatd()函数中包含两种熵指标：

字段名	函数调用	说明
`Entropy`	`entropy(seqdata)`	非标准化熵值
`Entropy.T`	`entropy(seqdata, norm=TRUE)`	标准化熵值(除以最大可能熵log₂n)

其中，标准化熵(Entropy.T)将熵值压缩到0~1范围，便于跨序列比较。Entropy.T值接近1表示状态分布均匀(复杂)，接近0表示状态高度集中(简单)

小结：

熵是分布的复杂度：衡量状态分布的均匀程度
不考虑顺序：仅关注”用了多少种状态、各占多少比例”
状态越集中，熵越低：一个状态主导整个序列→熵低(简单)
状态越分散，熵越高：状态多且出现次数平均→熵高(复杂)
极端情况下：如果同一时间点所有人都处于同一状态，熵 = 0；如果各种状态均匀分布，熵 = 最大值