前言#
在社会序列分析中,我们常常希望度量不同个体“人生轨迹”的相似性。除了传统的编辑距离方法(如 OM),我们还有一种更加“结构导向”的方法 —— 把序列按时间切成若干段,在每段中统计状态比例,拼接为一个超长向量,再使用欧几里得距离或卡方距离比较个体之间的差异。
在这个教程中,我们将用 Python 实现一个干净简洁的滑窗版本,它不同于 R 中 TraMineR 的那套“额外加一段 + 不对称补尾”的处理方式,更贴近实际理解。
TraMineR 的窗口切分逻辑简析#
有同学问如下问题:
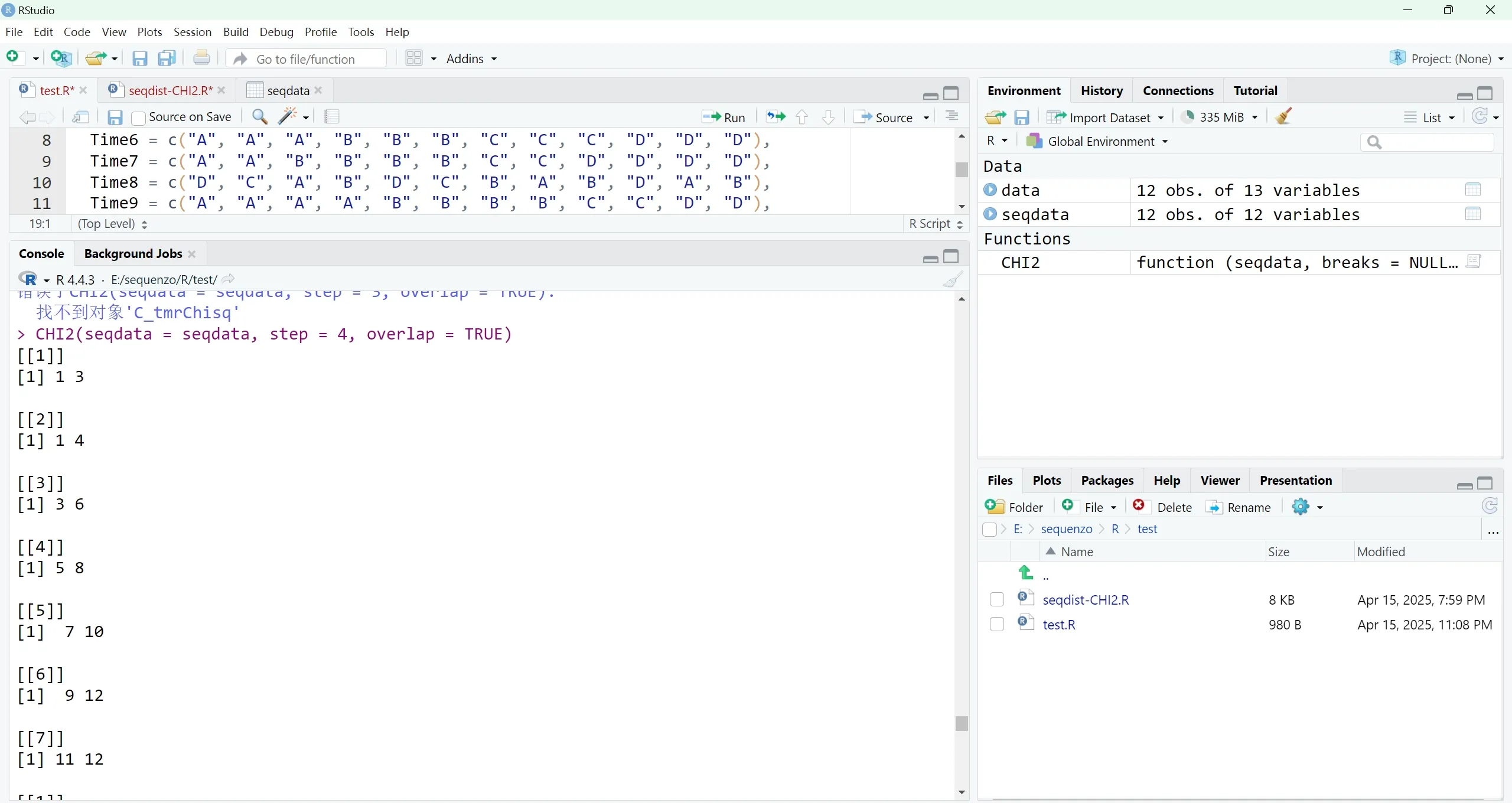
为什么对一个列数为12的seqdata切分,step=4,overlap=TRUE,会切成这样?
TraMineR的代码逻辑是会切成这样,后面的代码也还是拿着这样的分段继续计算,是overlap的规则就像它这样,还是TraMineR包写得草率了
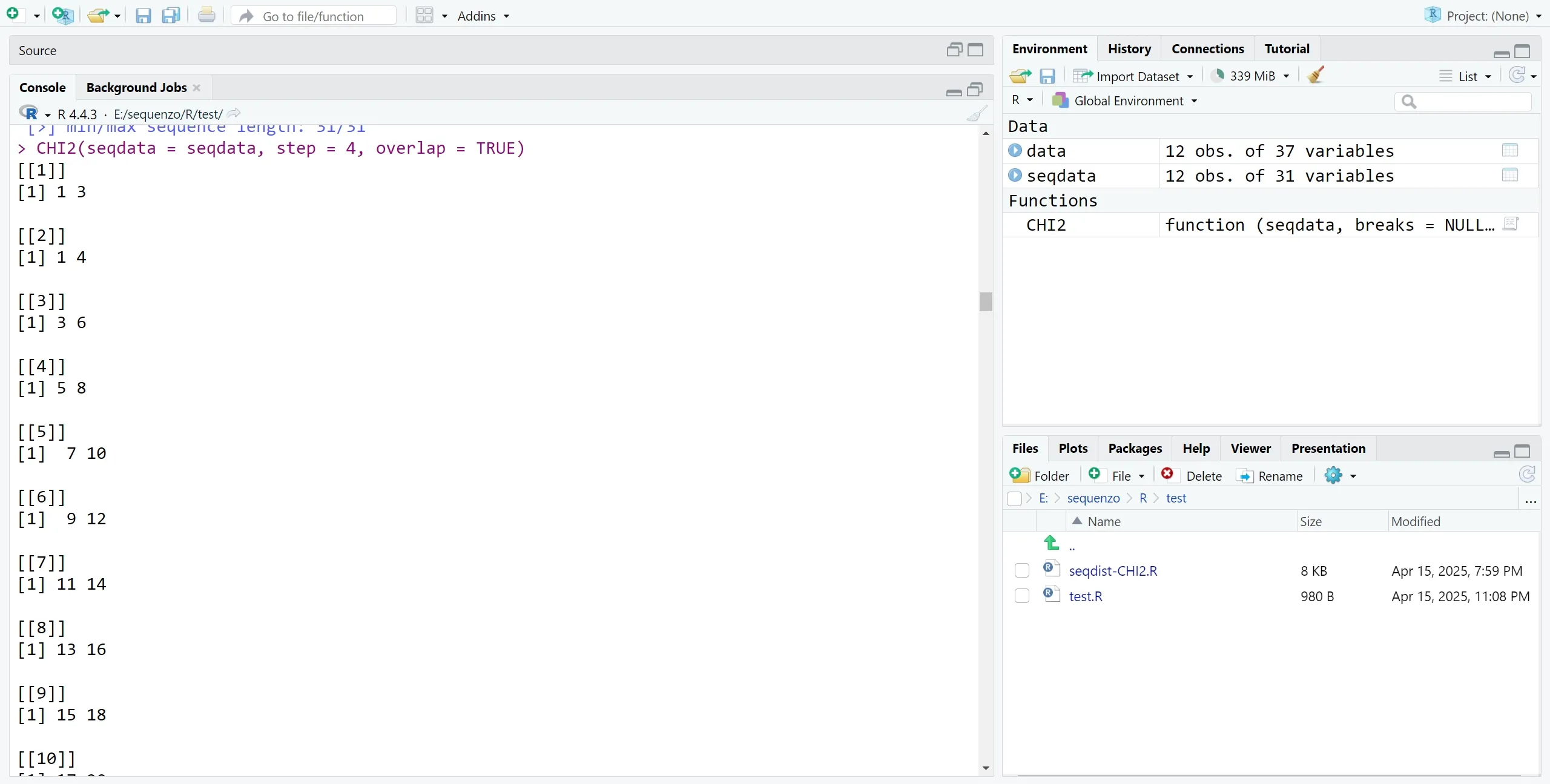
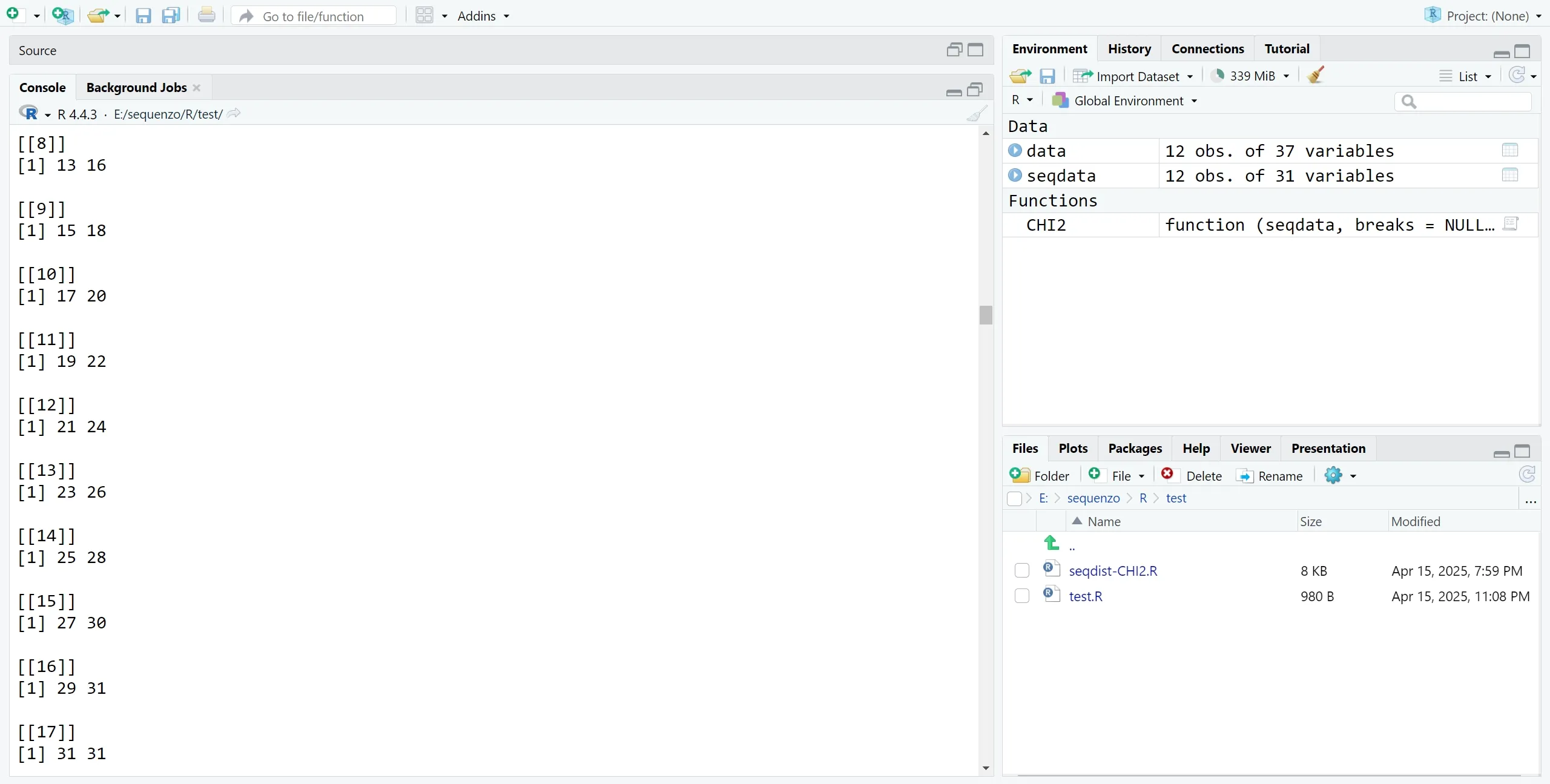
列数更高的时候(这里是31),也是切得怪怪的,不能保证每个段一样长
在 TraMineR 中,CHI2() 函数在 breaks=NULL 且 overlap=TRUE 时,会使用一种特殊的窗口生成方式。
给定一个序列长度为 12,step=4,overlap=TRUE,其切出来的窗口不是我们习惯的:
[1–4], [3–6], [5–8], [7–10], [9–12]而是:
[1–3], [1–4], [3–6], [5–8], [7–10], [9–12], [11–12]这是因为 TraMineR 在源码中:
- 手动加了一个额外“头段”
[1, step/2],用于捕捉序列开头的状态突变; - 每一个正常主段之后,再补一个
[start+step/2, end+step/2]的滑窗段; - 最后,如果还剩一点时间点(不足一整个窗口),也会强行补出一段末尾段。
这种划法是“密集覆盖”但带来了:
- 不对称窗口分布;
- 不一致的段长;
- 对时间点权重不均。
这不是滑窗标准做法,也不是论文建议逻辑,仅是 TraMineR 的特殊实现。
从截图重现 TraMineR 实际切段逻辑(ncol = 12, step = 4, overlap = TRUE)#
我们的输出是:
[[1]] 1 3[[2]] 1 4[[3]] 3 6[[4]] 5 8[[5]] 7 10[[6]] 9 12[[7]] 11 12这不是简单的 [1–4], [3–6], ... 加个头段,而是它不仅加了头段,还“穿插地”在每个主段之后加半段,而且最后还疯狂补尾
我们逐段拆解看看:
实际生成的 breaks:
| 段编号 | 起止位置 | 说明 |
|---|---|---|
| [1] | 1–3 | 手动加的头段 [1, step/2] = [1, 3] |
| [2] | 1–4 | 主段1(bb[1] 到 bb[2]-1 = [1, 4]) |
| [3] | 3–6 | overlap段1(= [1,4]+2) |
| [4] | 5–8 | 主段2(= [5,8]) |
| [5] | 7–10 | overlap段2(= [5,8]+2) |
| [6] | 9–12 | 主段3 |
| [7] | 11–12 | overlap段3(尾巴残段) |
所以 TraMineR 的实际策略是:
正常滑窗段:[1–4], [5–8], [9–12]
每段之后加个
[start+2, end+2]的重叠段开头硬加一段
[1, 3]尾巴如果剩几个时间点,继续切(不管长度是否符合 step)
总结它的逻辑是:
TraMineR (overlap=TRUE) = [头段] + [主段1, 主段1移位段] + [主段2, 主段2移位段] + [主段3, 主段3移位段?] + ...直到打满结尾再小结一下:
TraMineR 在
overlap=TRUE时的窗口划分逻辑并非传统“等步长滑窗”,而是一种嵌套的补段策略:
- 会额外添加一段开头
[1, step/2]- 每段后补一个“向右平移 step/2 的段”
- 尾部时间点不够也会继续强行切段
这种划法虽然覆盖密集,但段长不一致、时间点权重不均,不利于标准化与解释,因此在 Python 实现或教学时,我们采用更规则的滑窗方式:
[1–4], [3–6], [5–8], [7–10], [9–12]Python 教程中的标准实现方式#
我们遵循更清晰的逻辑:
def generate_windows(length, step=4, overlap=True): stride = step // 2 if overlap else step windows = [] for start in range(0, length - step + 1, stride): windows.append((start, start + step - 1)) return windows它输出的是标准的滑窗切段:
[(0, 3), (2, 5), (4, 7), (6, 9), (8, 11)]对比总结表格#
| 比较维度 | Python 教程滑窗法 | TraMineR overlap=TRUE 实现 |
|---|---|---|
| 是否加额外段 | ❌ 否 | ✅ [1, step/2] 补丁段 |
| 切分方式是否一致 | ✅ 是 | ❌ 每段长度不统一 |
| 是否标准滑窗逻辑 | ✅ 是(机器学习/信号处理常见) | ❌ 否,特殊实现 |
| 是否易于解释 | ✅ 是 | ❌ 难以直观理解 |
建议
- Python 实现推荐只保留长度一致的窗口,保证结构清晰;
- TraMineR 的逻辑可作为“历史兼容性”例子讨论,但不建议照搬;
- 若想保留其行为,可设置
prepend_half_window=True与allow_incomplete_tail=True参数。
后续内容可继续扩展:
- 加入卡方距离计算方式
- 扩展 missing value 支持
- 图示滑窗 vs 补丁段覆盖情况(可配合 matplotlib)
我们需要遵循的基本流程#
我们遵循下面这四个步骤:
切段 → 转状态比例向量 → 拼接 → 计算欧几里得距离
第一步:定义滑窗划段函数 generate_windows#
注意:下面的函数我写的都是中文注释,但在实际的开发中,需要写英文。
def generate_windows(length, step=4, overlap=True): """ 将一个序列长度切成若干时间段窗口,用于后续状态分布计算。
参数: length (int): 序列长度(即时间点数量) step (int): 每个窗口的长度 overlap (bool): 是否重叠(滑窗)
返回: List[Tuple[int, int]]: 每个窗口的起止索引(从0开始,含头含尾) """ windows = [] stride = step // 2 if overlap else step for start in range(0, length - step + 1, stride): windows.append((start, start + step - 1)) return windows示例:
generate_windows(length=12, step=4, overlap=True)# 输出:[(0, 3), (2, 5), (4, 7), (6, 9), (8, 11)]第二步:计算每个窗口的状态比例向量#
from collections import Counter
def state_distribution(window_seq, state_set): """ 将一个窗口内的状态序列转换为状态比例向量。
参数: window_seq (List[str]): 这个窗口中的状态列表 state_set (List[str]): 所有可能状态的全集(确保顺序统一)
返回: List[float]: 每种状态的比例(向量) """ counter = Counter(window_seq) total = len(window_seq) return [counter[state] / total for state in state_set]示例:
state_distribution(['A', 'A', 'B', 'C'], ['A', 'B', 'C'])# 输出:[0.5, 0.25, 0.25]第三步:拼接每段的状态比例向量#
def sequence_to_vector(seq, state_set, step=4, overlap=True): """ 把整个状态序列转换成一个拼接好的超长状态向量。
参数: seq (List[str]): 原始状态序列 state_set (List[str]): 所有可能状态 step, overlap: 切段控制
返回: List[float]: 超长拼接状态比例向量 """ windows = generate_windows(len(seq), step, overlap) segments = [] for start, end in windows: window_seq = seq[start:end + 1] dist = state_distribution(window_seq, state_set) segments.extend(dist) return segments示例:
sequence_to_vector(['A', 'A', 'B', 'C', 'B', 'B', 'C', 'C', 'A', 'A', 'B', 'C'], ['A', 'B', 'C'])那这个 sequence_to_vector() 函数会返回什么结果呢?
我们有如下输入信息:
seq = ['A', 'A', 'B', 'C', 'B', 'B', 'C', 'C', 'A', 'A', 'B', 'C']state_set = ['A', 'B', 'C']step = 4overlap = True这个序列长度是 12,设置的窗口长度是 4,并开启了 overlap。那么,滑窗窗口为:
[0–3] → A A B C[2–5] → B C B B[4–7] → B B C C[6–9] → C C A A[8–11] → A A B C共 5 段,每段长度为 4。
每段状态分布(按 A, B, C):
| 窗口 | 内容 | 分布结果 |
|---|---|---|
| [0–3] | A A B C | A:2/4, B:1/4, C:1/4 → [0.5, 0.25, 0.25] |
| [2–5] | B C B B | A:0, B:3/4, C:1/4 → [0.0, 0.75, 0.25] |
| [4–7] | B B C C | A:0, B:2/4, C:2/4 → [0.0, 0.5, 0.5] |
| [6–9] | C C A A | A:2/4, B:0, C:2/4 → [0.5, 0.0, 0.5] |
| [8–11] | A A B C | A:2/4, B:1/4, C:1/4 → [0.5, 0.25, 0.25] |
拼接结果:
将 5 段的比例向量拼接成一个超长向量:
[0.5, 0.25, 0.25, 0.0, 0.75, 0.25, 0.0, 0.5, 0.5, 0.5, 0.0, 0.5, 0.5, 0.25, 0.25]最终输出:
[0.5, 0.25, 0.25, 0.0, 0.75, 0.25, 0.0, 0.5, 0.5, 0.5, 0.0, 0.5, 0.5, 0.25, 0.25]长度为 5 段 × 3 状态 = 15 维。
当然,如果你想要让内容更具体且容易理解,也可以用一个函数帮助 打印每段内容和比例:
def show_window_vectors(seq, state_set, step=4, overlap=True): windows = generate_windows(len(seq), step, overlap) for i, (start, end) in enumerate(windows): window_seq = seq[start:end+1] vec = state_distribution(window_seq, state_set) print(f"[{start+1}-{end+1}] {window_seq} -> {vec}")运行:
show_window_vectors(seq, ['A', 'B', 'C'], step=4, overlap=True)第四步:计算欧几里得距离(L2 距离)#
import numpy as np
def euclidean_distance(vec1, vec2): return np.linalg.norm(np.array(vec1) - np.array(vec2))示例:
euclidean_distance([0.5, 0.3, 0.2], [0.3, 0.5, 0.2])# 输出 ≈ 0.28然后再批量计算所有个体之间的距离矩阵:
def compute_distance_matrix(sequences, state_set, step=4, overlap=True): """ 计算所有个体状态序列之间的欧几里得距离矩阵。
参数: sequences (List[List[str]]): 所有个体的状态序列列表 state_set (List[str]): 状态全集
返回: 2D NumPy array: 距离矩阵 """ vectors = [sequence_to_vector(seq, state_set, step, overlap) for seq in sequences] n = len(vectors) matrix = np.zeros((n, n)) for i in range(n): for j in range(i + 1, n): dist = euclidean_distance(vectors[i], vectors[j]) matrix[i][j] = matrix[j][i] = dist return matrix小结#
| 步骤 | 函数名 | 说明 |
|---|---|---|
| 1️⃣ 切段 | generate_windows | 根据 step 和 overlap 划时间窗口 |
| 2️⃣ 单段比例 | state_distribution | 每段状态比例向量 |
| 3️⃣ 拼接全序列 | sequence_to_vector | 拼接多个段落为超长向量 |
| 4️⃣ 距离计算 | euclidean_distance + compute_distance_matrix | 得到所有人的距离矩阵 |
注意事项 & 扩展建议
- 【重要】是否可以进行标准化? 你可以除以
sqrt(#segments)来标准化不同step的距离(TraMineR 里叫norm=TRUE)。 - 【重要】向量维度要保持一致:所有人的状态全集
state_set必须一致、顺序固定。 - 【重要】支持缺失值:可扩展
state_distribution()支持None或"NA"。 - 支持多种距离:如果学有余力,还可以加上 L1, L∞, Cosine 等做比较,真正掌握这些距离,明晰它们的区别和联系。
作业:
比较和讲解不同
step和overlap设置下距离矩阵的变化试着开始做 Python 的代码,将各个逻辑点连成一片,也可以试着做流程图,让自己的思路更清晰