主流的编辑距离算法之外的社会距离计算 2.1：欧几里得距离的数学与应用

前言：最简单的距离，为什么最耐用？#

在我们学习社会序列分析时，可能会以为“欧几里得距离”只是最基础的知识，没什么特别。但不知读者有没有想过，一个公元前 300 年的几何公式，为什么还能出现在我们分析当代社会轨迹的模型中？

这不是偶然，而是因为：

它的直觉性很强：“两点之间的最短距离是直线”，人人都懂；
它的数学性很好：满足勾股定理、三角不等式、连续可导等性质；
它的适应性很广：二维地图、三维建模、高维状态空间，一套公式走天下；
它的算法性也很稳：被无数模型默认使用（如 K-means、PCA、KNN、神经网络等）

甚至可以说，欧几里得距离是“所有现代距离度量的祖师爷”。

而在社会科学中，当我们把一个人的一生、一个家庭的变迁、一个群体的轨迹，转化为向量化的状态数据后，我们仍然绕不开这个最基础、却最强大的度量方式。

本篇教程将带你重新认识这位“老朋友”：

它的起源：从欧几里得几何到现代坐标空间
它的数学本质：范数、向量、空间结构（对学习机器学习和深度学习都非常非常重要）
它的可视化解释：从三角形斜边到高维空间距离

下一篇教程中，我们会重点讲解：

它的社会科学应用：为什么它在社会序列分析中依然很重要，并且以 TraMineR 包为例给大家讲解；
它的局限与转向：什么时候我们应该选择它，又什么时候该超越它？

在机器学习、图像识别、基因比对之外，欧几里得距离在社会科学中的生命力，远比我们想象得更深远。

现在，就让我们从一张纸上的两个点开始，重新出发。

目录#

一、欧几里得距离的源起：最古老的度量方式之一
二、从坐标到欧几里得空间
- 为什么要引入“欧几里得空间”？
- 欧几里得空间 vs 非欧空间
三、有这么多距离范数，为什么我们要选欧几里得范数（L2）？
加餐：什么是“向量”？什么是“分量”？

一、欧几里得距离的源起：最古老的度量方式之一#

欧几里得距离（Euclidean Distance）得名于古希腊数学家 Euclid（欧几里得），他在公元前 300 年左右，编写了一部划时代的数学著作《几何原本》（英文名 Elements）。这本书一共包含13卷，被称为人类历史上最成功、影响最深远的教科书之一。它系统地整理了古希腊数学知识，提出了“公理-定理”的证明体系，对后来的科学、数学、甚至哲学都产生了巨大影响。

其中，欧几里得距离最早就是在这本书的平面几何部分中，用来衡量两个点之间的“直线距离”。

什么是“几何”？什么是“平面几何”？#

“几何”这个词来自希腊文 geo（大地） + metron（测量），意思就是“测量大地”。

最初，几何学是为了帮助人们：

测量土地（古埃及尼罗河泛滥后重新划分地块）；
计算面积、角度；
修建房屋、绘制地图；

也就是说，几何学是研究“形状、空间、位置、大小和相互关系”的学科。

几何主要回答以下问题：

几何问题	举例
距离是多少？	两点之间的最短距离（如欧几里得距离）
面积是多少？	一个三角形或圆的面积
两条线相交吗？	判断线段、角度关系
角度是多少？	直角、钝角等的测量
一个形状可以变换成另一个吗？	图形旋转、平移、对称等

那什么是“平面几何”？（Plane Geometry）#

平面几何是几何学中的一个分支，它只研究发生在二维平面上的形状和关系。

特征：

所有图形都在一张平面纸上（二维）；
不考虑“厚度”或“高度”；
使用的对象包括：点、线段、直线、角、三角形、圆、多边形等；

如果读者还记得的话，这些都是中学几何课的主要内容。我们再举几个“平面几何”研究的问题：

点 A 到点 B 有多远？
一个三角形的三个角加起来等于多少度？（答案是 180°）
两条直线在什么情况下相交或平行？
一个圆的面积是多少？
如何通过两点确定一条直线？

欧几里得在《几何原本》中主要研究的，就是这种平面几何，也叫作欧几里得几何。

概念	解释	举例
几何（Geometry）	研究形状、空间、位置、距离的数学学科	建房子、导航、画地图
平面几何（Plane Geometry）	研究“二维空间”中点、线、面之间关系	三角形、圆、直角、距离公式等
欧几里得距离	平面几何中最基本的概念之一：两点之间的最短距离	$D = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$

平面几何就像是在一张白纸上讨论“点和线”的世界，而欧几里得距离，就是这个世界中最基础、最简单、却也最重要的一个度量单位。

欧几里得距离公式的几何含义#

我们从二维空间开始：

设有两个点：

$x = (x_1, x_2)$
$y = (y_1, y_2)$

它们之间的距离就是：

D(x, y) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2}

这正是初中数学中的勾股定理（Pythagorean theorem），意思是：两点之间的最短路径 = 连线形成的直角三角形的斜边。

你可能会问，为什么 $D(x, y) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2}$ 代表“最短路径”？

想象一个简单的二维坐标系，我们还是有同样的两个点：

$x = (x_1, x_2)$
$y = (y_1, y_2)$

注意：

当我们写 x = (x₁, x₂) 时，它表示的是一个点在二维平面坐标系中的位置，而不是“两个 x 值”或“都在 x 轴上的数”。这个写法来自数学中的“向量”或“点坐标”表示法。
在这个表示中，x₁ 是点的横坐标（也就是 x 轴方向的位置），x₂ 是纵坐标（也就是 y 轴方向的位置）。比如：点 x = (3, 4) 表示“从原点向右走 3 格，再向上走 4 格”。
初学者很容易误解为 x₁ 和 x₂ 都是 x 的数值，好像它们都在 x 轴上。其实不是这样，它们分别表示在两个维度上的坐标，就像“横着多少”和“竖着多少”。
总结一句话：(x₁, x₂) 是一个点的完整“地址”，第一维是横向（x轴），第二维是纵向（y轴）。这个格式也适用于三维空间，比如 (x, y, z) 表示 3D 空间中的一个点。
我们之所以在这里写 (x₁, x₂)，是因为它表示 x 的第一个值为 x₁，x 的第一个值为 x₂。

再回到我们的这两个点的例子中，你可以在纸上画出这两个点，然后连接它们，形成一条线段。

具体而言，如果你从 $x$ 沿着横轴（x 轴）水平走到 $y$ 的“垂直位置”，再垂直向上走到 $y$ ，你就画出了一个直角三角形：

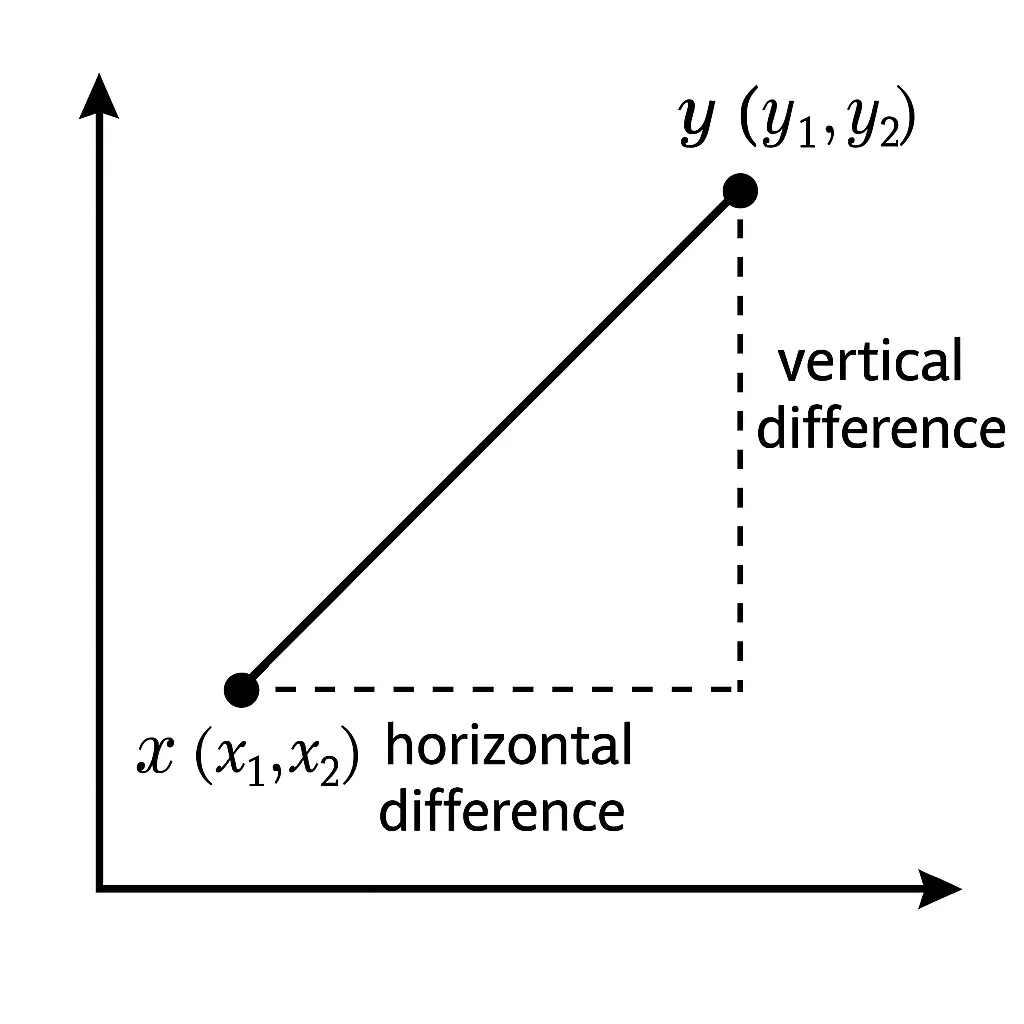
euclidean-distance-img

这个三角形的两条直角边就是：

横向差（Horizontal difference）： $|x_1 - y_1|$ （水平边长）
纵向差（Vertical difference）： $|x_2 - y_2|$ （垂直边长）

所以，这两个点之间的线段（即“最短路径”）就是这两个边组成的直角三角形的斜边，根据勾股定理：斜边² = 邻边² + 对边²

也就是：

\text{距离}^2 = (x_1 - y_1)^2 + (x_2 - y_2)^2

取平方根就得到了两点之间的距离公式：

D(x, y) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2}

延伸到 n 维空间：

D(x, y) = \sqrt{ \sum_{i=1}^n (x_i - y_i)^2 }

这就变成了我们在数据分析中最常用的距离度量方式。

二、从坐标到欧几里得空间#

这个公式其实是欧几里得几何空间中定义距离的标准方式。你可能会问：“为什么非得搞一个‘欧几里得空间’的概念？直接说平面、三角形不就行了吗？”

这是很多人在学习数学、线性代数、空间距离时会有的疑问。简而言之：

“欧几里得空间”听起来有点吓人，其实就是我们日常所理解的“直角坐标系空间”，它的本质特征是可以使用勾股定理来计算距离。
在这个空间里，我们可以用向量的方式来表示点，点与点之间的“最短路径”就是向量差的模，也就是我们熟悉的“斜边长度”。
引入“欧几里得空间”这个词，是为了在数学上统一处理不同维度、不同坐标系统下的距离问题，方便推广、泛化和理论建模。

那么，具体该如何理解呢？

首先，其实我们已经在用“欧几里得空间”了。当我们在二维平面上说：

两点之间的距离 = $\sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2}$

这个就是欧几里得空间里的距离定义。只不过我们平时不说“欧几里得”，就直接当作生活常识用了。

那“欧几里得空间”这个词是啥意思？欧几里得空间（Euclidean space）只是一个数学语言中对“我们习惯的空间”的正式称呼。

它满足下面这些特性：

特性	意义
有坐标轴	像 $x, y, z$ 一样的直角坐标轴
有方向与距离	点与点之间可以测量“多远”
满足勾股定理	形成三角形时，斜边² = 两直角边²
向量加法、数乘有意义	$v + w$ 、 $2v$ 这些操作能正确解释空间位置

所以，“欧几里得空间” = 有坐标、有方向、有勾股定理可用的那种熟悉的几何空间

比如：

你画图的那张图，是二维欧几里得空间 $\mathbb{R}^2$
如果你是 3D 游戏建模，那就是三维欧几里得空间 $\mathbb{R}^3$
如果你有 10 个维度的状态，那就是 $\mathbb{R}^{10}$ ，也是欧几里得空间

注意： $\mathbb{R}$ 是数学中表示“实数集”的标准符号，它采用了一种叫做黑板粗体（blackboard bold）的字体风格，用来强调这个符号代表的是一个特殊集合，而不是普通变量。

实数集包含了所有我们熟悉的连续数，比如：

... -3, -2.5, 0, 1.414, π, e, 1000.002 ...

这种黑板粗体（blackboard bold）起源于美国大学讲课的时代，教授们在黑板上写字时，为了区分一些“特别重要的集合符号”，会故意加两笔竖线，表示：

$\mathbb{R}$ ：Real numbers（实数）
$\mathbb{N}$ ：Natural numbers（自然数）
$\mathbb{Z}$ ：Integers（整数，来自德语 “Zahlen”）
$\mathbb{Q}$ ：Rational numbers（有理数，来自 “Quotient”）
$\mathbb{C}$ ：Complex numbers（复数）

我们为什么要引入“欧几里得空间”这个概念？而不是只说“二维平面”？#

这是为了推广和统一数学语言。

我们可以这样理解：

我们口语说的	数学里的版本
画在纸上的平面	欧几里得空间 $\mathbb{R}^2$
空间中两个点的距离	向量之差的欧几里得范数
勾股定理	范数公式 $\\|x - y\\| = \sqrt{\sum (x_i - y_i)^2}$
两个点之间的最短路径	欧几里得距离（Euclidean distance）

也就是说，欧几里得空间是数学用来“抽象地描述所有这类空间”的统一概念，不管你是二维的、三维的，甚至是 100 维的，它都能用统一方式处理。

打个通俗比方，想象你写代码时，经常要对人、动物、车辆做处理，如果你把它们都抽象成一个“对象”，那你就可以写：

for obj in all_objects:
    obj.move()

而不是：

for person in people:
    person.move()
for animal in animals:
    animal.move()

欧几里得空间的作用就是这种“数学抽象统一”：你不管分析 2D 空间、3D 空间、10D 向量空间，用的都是同一个范数、一个公式、一个几何思想。

那么，结合我们这个小节和上个小节所说的，不妨来再来理解一下，这个3D欧几里得空间即 $\mathbb{R}^3$ 是什么意思？

$\mathbb{R}^3$ 并不是“3个实数”或者“实数的三次方”，而是三维欧几里得空间（3-dimensional Euclidean space），用数学语言表达就是：所有三维实数向量组成的集合。

它的意思是：

所有可以写成 $(x, y, z)$ 的三维坐标点，
其中 $x, y, z \in \mathbb{R}$ （都是实数）

具体拆解一下 $\mathbb{R}^n$ 的含义：

$\mathbb{R}$ 表示实数集合
比如 $x = 2.5$ 、 $y = -3.14$ 、 $z = \sqrt{2}$ 都属于 $\mathbb{R}$
$\mathbb{R}^n$ 表示的是长度为 $n$ 的实数向量空间
也就是 $n$ 维坐标系统中的所有可能的点（每个点有 $n$ 个坐标值）

我们再做一个对比：

表达式	含义说明	对应空间
$\mathbb{R}^1$	所有实数点，数轴上的一条线	一维直线
$\mathbb{R}^2$	所有 $(x, y)$ 实数点，组成平面	二维平面（如地图、画布）
$\mathbb{R}^3$	所有 $(x, y, z)$ 实数点，组成三维空间	三维空间（如 3D 模型、地球）
$\mathbb{R}^{10}$	所有含 10 个实数的向量	十维空间（常用于机器学习）

那为什么我们说 $\mathbb{R}^3$ 是一个“欧几里得空间”？

因为在这个空间里：

有坐标轴（ $x, y, z$ ）
点与点之间的距离可以用欧几里得距离公式来算：

\text{距离} = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + (x_3 - y_3)^2}

满足我们熟悉的几何规则（如勾股定理、平移不变、直线最短等）

这就构成了一个三维欧几里得空间 $\mathbb{R}^3$ ：“用实数来表达坐标，用直线来连接点，用勾股定理来计算距离的三维空间”。

小结：

在我们这里说的 $\mathbb{R}^3$ ，意思是“三维欧几里得空间”，
它包含了所有像 $(x, y, z)$ 这样的实数向量，是一个坐标可定义、距离可计算、符合直觉几何规则的空间。
这种表达方式也适用于更高维，比如社会状态向量在 $\mathbb{R}^{10}$ 中比较差异。

欧几里得空间 vs 非欧空间#

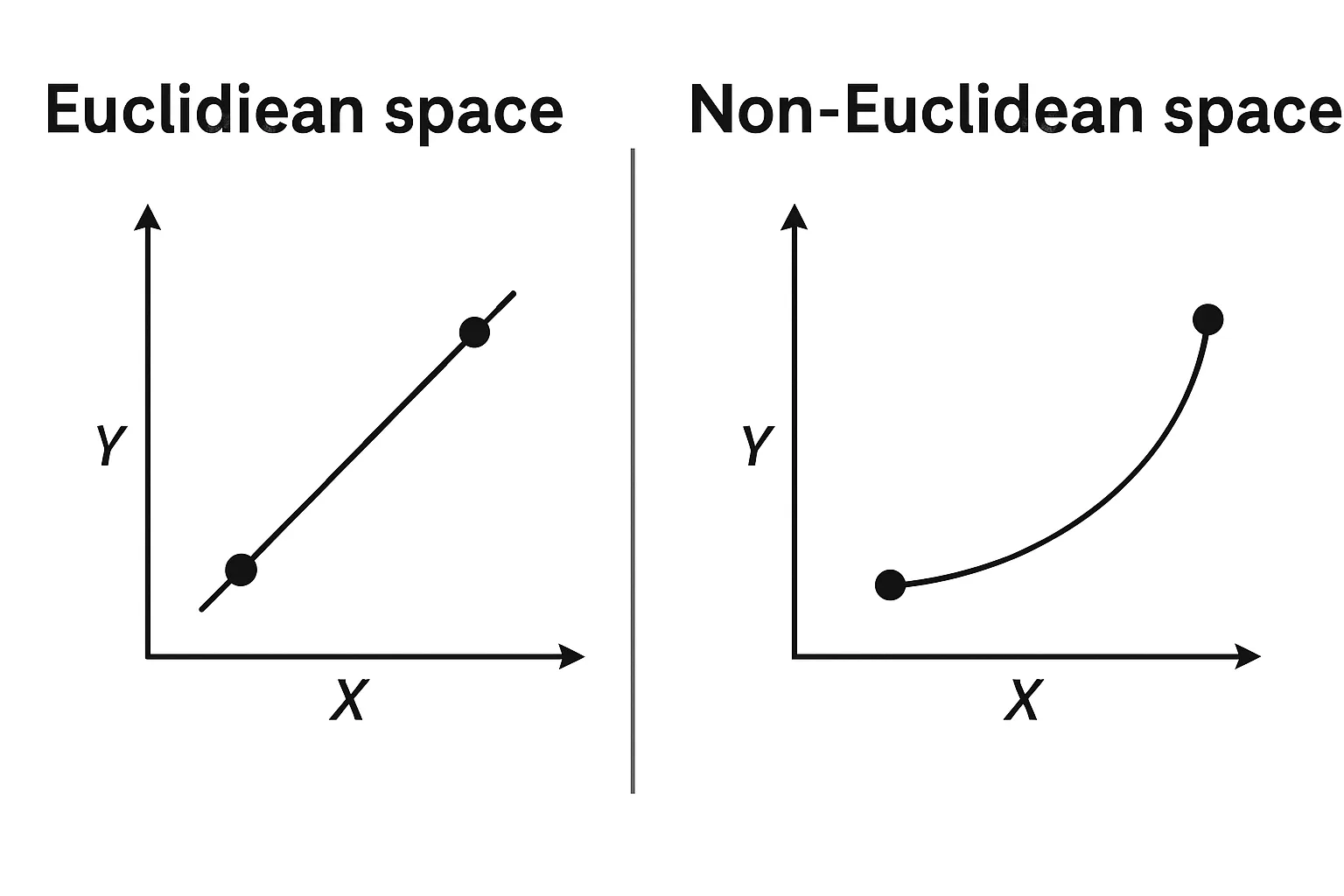
euclidean-distance-img

在上图中，我们直观地对比了两种截然不同的空间结构：

左侧：二维欧几里得空间（Euclidean Space）

你可以看到一个标准的、网格状的平面，坐标轴是互相垂直的直线，这就是我们最熟悉的空间形式，也就是高中数学里“直角坐标系”的抽象化表达。

在这个空间中：

点之间的最短路径是直线；
可以使用勾股定理来计算距离；
空间是“平的”、没有弯曲；
方向、角度和长度都有稳定的几何意义。

这种空间结构适用于我们平时的纸面几何、二维地图分析、数据空间可视化等常见情境。我们所说的“欧几里得距离”就是在这种空间中定义的。

右侧：非欧空间（Non-Euclidean Space）

右边则展示了一个弯曲的曲面空间，它可以是一种球面、鞍面或一般的曲率空间（图中简化成波浪形平面）。这类空间就属于非欧几何的范畴。

在这样的空间中：

点与点之间的最短路径（叫“测地线”）不再是直线，而是随曲率弯曲的弧线；
勾股定理不成立；
空间的结构受“弯曲程度”影响，方向感和角度定义可能会改变；
比如：在地球表面两点之间的最短路径是一段“大圆弧”而不是地图上的直线。

我们平时“假设”生活在欧几里得空间，是因为这在小尺度上非常接近现实、计算简单、直观易懂，相当于是一个简化的模型。
但严格来说，真实世界其实是非欧几里得的，尤其在大尺度、高速度、复杂结构中，这种假设会迅速失效。

那为什么我们可以平时“假设”生活在欧几里得空间呢？因为在日常生活的尺度范围内（比如城市、房间、小尺度地图），地球的曲率几乎感觉不到，重力场变化也很小，光速的限制也不会影响你走路、开车、购物。

所以我们才会自然地觉得：“两点之间的最短路径是直线”，“平行线永不相交”，“勾股定理一定成立”；而这些，都是欧几里得几何的核心公理。

正是因为这些假设在我们的经验中“没有出错”，于是我们把它当作理所当然的空间认知框架。

但是，在以下领域中，非欧几何就变得不可或缺：

应用领域	非欧空间的意义
地理学 / 导航	地球是球面，必须使用球面几何计算距离
广义相对论	引力使空间弯曲，不能再假设空间是“平的”
高维数据分析	某些复杂数据空间具有内在弯曲结构
某些社会科学	网络结构、时间路径、状态空间非线性变形

小结一句话：

欧几里得空间是“平的”，适合描述我们熟悉的直线距离；
非欧空间是“弯的”，适合描述现实中复杂、弯曲的结构世界。

为什么欧几里得距离能流行几千年？

原因	具体解释
几何直觉强	“最近的两点之间就是一条直线”，人人都能理解
数学性质好	连续、可导、满足三角不等式，是“度量空间”的基石
应用范围广	数据分析、图像处理、聚类算法、空间建模无所不在
高维可拓展	它不只适用于二维、三维空间，而是任意维度的“空间距离”概念
算法友好	很多算法如 PCA、t-SNE、KNN 都默认使用它作为基础距离计算方式

欧几里得距离不仅是最古老的距离度量方式之一，也是现代数据科学的核心工具之一。

它将“几何直觉”与“代数表达”结合，成就了一个横跨两千年数学史的超级公式，从欧几里得到笛卡尔，到高维向量空间，再到机器学习和社会科学序列分析，一个公式贯通古今。

三、有这么多距离范数，为什么我们要选欧几里得范数（L2）？#

在研究“两个序列有多相似”这个问题时，我们经常会把每个序列转换成一个向量，然后再去计算向量之间的“距离”。

比如，一个人生轨迹可以变成这样一个向量（如果你已经看了我们上一篇教程的话）：

工作：40%，失业：30%，照顾家庭：30% → 向量：[0.4, 0.3, 0.3]

那么问题来了：你怎么衡量两个这样的向量有多不一样？这就引出了一个数学核心概念——范数（norm）。

什么是范数？#

简单来说，范数（norm）就是衡量“一个向量有多大”或“两个向量相差有多远”的方法。它是数学中最常用的一种度量工具。

常见的范数属于 $L_p$ 范数家族，其一般形式为：

L_p(x, y) = \left( \sum_{i=1}^n |x_i - y_i|^p \right)^{1/p}

这条公式表示：

把两个向量之间的每一维的差值取 $p$ 次方，加起来，再开 $1/p$ 次方。

不同的 $p$ 值，就代表了不同的“距离感”。

我们一步步来拆解这个公式：

公式部分	含义
$x, y$	是两个 n 维向量（比如 `[3, 4]` 和 `[0, 0]`）
$x_i - y_i$	表示第 $i$ 个维度的差值
$绝对值(x_i - y_i)^p$	把差值的绝对值做 $p$ 次方，保证都是正数
$\sum_{i=1}^n \dots$	把所有维度的差值累加起来
$\left( \dots \right)^{1/p}$	最后开 $p$ 次方，完成“标准化”处理

本质上：这是在问 “x 和 y 有多不一样”，但用不同方式度量这个“不一样”。

我们可以看出来，其实说到底，范数衡量的还是两个点之间的距离，只不过是不同的范数（不同定义的规则）下，对距离有着不同的理解。
就像现实中从家到超市有不同的走法（比如走斜线 vs 沿街拐弯），不同的范数，就是不同的“走法规则”。

举个具体例子，我们来计算同一对向量在不同 $p$ 值下的距离。

设有两个二维向量：

$x = [3, 4]$
$y = [0, 0]$

我们来看：

L1 范数（曼哈顿距离）#

L_1(x, y) = |3 - 0| + |4 - 0| = 3 + 4 = 7

像是在城市街区里走的路线：走横的3格 + 走竖的4格 = 总共走了7个格子

这也是为什么我们叫它曼哈顿距离的原因，因为在纽约有个叫做曼哈顿的街区，这个街区地理规划都是像棋盘一样，街区都是一格一格的。因此，在这样的街区中行走，你只能横着竖着走，没办法斜着走（L2 欧几里得距离）。

L2 范数（欧几里得距离）#

L_2(x, y) = \sqrt{(3^2 + 4^2)} = \sqrt{9 + 16} = \sqrt{25} = 5

这是我们熟悉的直线距离，基于勾股定理，可以发现从 x 走到 y，直线的最短距离是 5。

L∞ 范数（最大距离）#

L_\infty(x, y) = \max\{ |3|, |4| \} = 4

只关注哪个维度差得最远，也叫“切比雪夫距离”。

那“4”代表什么？

根据 x 和 y 的坐标，两个维度的差是：

第一维（横向走）： $|3 - 0| = 3$
第二维（纵向走）： $|4 - 0| = 4$

所以，根据公式

L_\infty = \max\{3, 4\} = \boxed{4}

这意味着，在两个点之间，最“难跨越”的一个维度的差值是 4。

切比雪夫距离在国际象棋中也很常见：

棋盘上的“国王”，每一步最多只能往一个方向移动一格（可以对角、也可以直走）；
从 $(0,0)$ 到 $(3,4)$ ，最少也要走 4 步，因为你一次只能“对角靠近一步”

你可能会问，为什么不是“总长度”或者“斜线”？

因为那是其他范数的思路：
- L2 范数（欧几里得距离）是斜边思维，计算从 $x$ 到 $y$ 的真实最短直线距离；
- L1 范数（曼哈顿距离）是总成本思维，表示你在所有维度上“加起来”走了多少；
- L∞ 范数是最坏情况思维，意思是：不管其他维度多好，我只看最难的一维要走多远，因为任务的瓶颈决定一切。

使用场景

机器控制系统：哪个轴运动得最慢，决定了任务完成的总时间
- 比如，一个多轴控制的机器臂要在 $x$ 和 $y$ 两个方向同时移动， $x$ 轴要走 3 单位， $y$ 轴要走 4 单位，但两个轴的马达不能协同加速，只能匀速运动，而任务只有在最慢的轴也完成动作时才算结束。
- 这时候，总时间 = max(3, 4) = 4 秒。也就是说：最慢的那一维，拖慢了整体任务的完成时间。
网格游戏路径规划
容差分析：检测哪个维度的误差最大
棋盘类策略建模（国际象棋、围棋AI等）

小结一下，对比不同范数的感知方式：

范数	例子值	直觉意义
L1	7	所有方向加起来有多远（街区距离）
L2	5	实际直线距离（最短路径）
L∞	4	最大一维的差距（最坏情况）

也就是说: $L_p$ 范数就是要我们问自己，我们到底想如何感受差异？是全部加起来？只看最远的那个维度？还是权衡整体形状？

比如我们从家走到超市，有不同的走法：

如果你想从家到超市走得最近，选 L2；
如果你只能直走或转弯，像在棋盘上走路，选 L1；
如果你只关心最难走的一步，选 L∞。

现在我们知道了有各种各样的范数，但是为什么欧几里得距离（L2）最常用呢？#

欧几里得范数，就是 $L_2$ 范数，它的计算公式是：

\|x - y\|_2 = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \cdots}

也就是我们在二维空间里熟悉的“直线距离”或“斜边长度”。

它的优势主要体现在以下几个方面：

优势类别	原因解释
几何意义直观	它对应的是我们直觉上的“最短路径”，也就是两个点之间的直线，符合勾股定理
方向感更稳定	比 L1 更能体现“整体差异方向”，不会被维度的正负号抵消
计算优化友好	是连续可导函数，在机器学习/优化中非常好用
算法兼容性好	是很多算法默认距离度量，如 K-Means、SVM、PCA 等
不偏不倚	不像 L1 强调稀疏，也不像 L∞ 只关注极端值，L2 在整体结构上更“平均”
可以定义内积空间	也就是说它不仅能算距离，还能定义“角度”、“正交”、“投影”等概念

L2 范数（欧几里得距离）几乎出现在所有与“距离”、“误差”、“最优解”有关的算法或建模思路中。

1. 误差衡量：L2 损失函数（最小二乘）#

应用场景：

线性回归
神经网络中的 MSE（均方误差）
时间序列预测
信号还原

举例：在线性回归中，我们用 L2 损失来度量真实值 $y$ 和预测值 $\hat{y}$ 的差异：

\text{Loss}_{L2} = \sum (y_i - \hat{y}_i)^2

优点：

可导，适合反向传播；
惩罚大误差 → 模型更关注预测不准的地方；
数学分析性强，解可以解析求得。

2. 聚类分析：K-means 算法#

应用场景：

客户细分
图像压缩
文本主题聚类（向量空间）
生物数据聚类（如基因表达）

为什么用 L2？

K-means 的核心是最小化样本点到聚类中心的欧几里得平方距离：
$\sum_{k=1}^K \sum_{x_i \in C_k} \|x_i - \mu_k\|_2^2$
欧几里得距离与“向量空间中的均值”匹配良好，能快速迭代并找到最优聚类。

3. 降维分析：主成分分析（PCA）#

应用场景：

数据可视化
特征压缩
去噪处理

和 L2 的关系： PCA 的目标是找出保留最大方差（也就是最小 L2 重构误差）的投影方向：

在欧几里得空间中找出最佳投影，使得：
$\min \|X - X_{\text{projected}}\|_2^2$

4. 最近邻算法（KNN）中的距离计算#

应用场景：

分类预测（KNN）
推荐系统（基于相似度）
异常检测

为什么常用 L2？

L2 作为“物理空间中的直线距离”最直观；
特别适合数值型向量（如图像像素、用户打分等）；
计算效率高，可加速（如使用 KD-Tree）。

5. 图像处理与计算机视觉#

应用场景：

图像相似度度量
图像去噪（Total Variation Regularization 中常搭配 L2）
特征匹配（如 SIFT 特征之间的 L2 距离）

举例：

比较两张人脸特征向量之间的距离；
使用 L2 匹配图像块进行修复；
神经网络中用 L2 loss 训练去噪自编码器。

6. 正则化项：Ridge Regression（L2 正则）#

应用场景：

防止模型过拟合
回归参数收缩
稳定性增强（尤其是共线性场景）

正则项：

\text{Loss} = \text{MSE} + \lambda \sum \theta_i^2

惩罚参数幅度，使模型“更保守”；
结果是系数更平滑，但不会变成 0。

L2 范数在哪些问题中最适用？

应用方向	使用方式	为什么用 L2？
回归模型	L2 损失	关注大误差，导数光滑
聚类分析	距离计算	快速可导，适合均值
降维压缩	重构误差	提供最小整体偏差方向
图像处理	特征距离	视觉向量空间中最自然
模型正则化	参数缩小	保留全部特征，控制复杂度

一句话总结：L2 范数适用于你关心整体误差、喜欢“光滑变化”、强调最短路径、或模型要可导、好优化的场景。

加餐：什么是“向量”？什么是“分量”？#

我们在坐标图中经常会看到像 $x = (x_1, x_2)$ 这样的表达，很多人一开始可能会有点迷糊：为什么这个“x”后面有两个数？它们到底是什么？

其实，这种写法表示的并不是“两个 x 值”，而是一个二维空间里的向量（vector）。

向量是“有方向的量”#

你可以把“向量”想象成一支箭头，它有两个基本特征：

大小（magnitude）：箭头有多长
方向（direction）：箭头指向哪里

在二维空间里，一个向量通常表示“从某个起点出发，走多少横向 + 多少纵向”。

比如：

向量 $x = (3, 4)$ 表示：从起点向右走 3 格，再向上走 4 格

这个箭头就从原点 $(0, 0)$ 指向 $(3, 4)$ ，它的终点就是我们常说的“点的位置”。

分量是什么意思？#

向量有多个“方向上的分量”（components），也就是它在每个坐标轴上“贡献了多少”。

在二维空间里：

第一个分量 $x_1$ ：表示在 x 轴方向（横向）移动的距离
第二个分量 $x_2$ ：表示在 y 轴方向（纵向）移动的距离

所以我们说：一个向量是由多个“分量”组成的，每个分量告诉我们它在某一个方向上的“分布”或“投影”。

比如，向量 $(3, 4)$ 就是一个有两个分量的向量：3 是它的横向分量，4 是它的纵向分量。

为什么这很重要？#

在计算两点之间的距离时，我们其实就是在比较两个向量之间的差距（也就是从一个箭头指向另一个箭头的最短线段长度）。这时我们必须知道它们各自在 x 轴和 y 轴上“分别走了多少” —— 也就是比较它们的“分量差”。

小结

向量是一种“有大小和方向的量”，它就像一个箭头
分量是这个箭头在每个坐标方向上的投影
所以 $(x_1, x_2)$ 表示的是“横向 $x_1$ ，纵向 $x_2$ ”的一个向量，它也可以代表一个点在平面上的位置，因为它们在本质上是一样的